Основные законы магнитной цепи.

Задачей расчета магнитной цепи является: 1) определение намагничивающей силы (н.с.) катушки, необходимой для создания рабочего потока заданной величины (прямая задача), 2) определение рабочего потока по известной н.с. катушки (обратная задача). Расчет магнитных цепей базируется на основных законах магнитной цепи. Их можно выразить, исходя из формальной аналогии с электрическими цепями, следующим образом.

Закон полного тока. Сумма магнитодвижущих сил, действующих в замкнутом контуре, равна полному току, охватываемому этим контуром

. (113)

Закон Ома. Магнитный поток Ф равен разности магнитных потенциалов U_m на каком-либо участке магнитной цепи, помноженной на магнитную проводимость этого участка G_m

Ф = U_mG_m или Ф =U_m/R_m.(114)

Магнитное сопротивление участка магнитной цепи из ферромагнитного материала равно

1/Г, (115)

где l – длина участка, м; S – площадь сечения участка магнитопровода, м²; 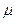– магнитная проницаемость материала, Г/м; G_м – магнитная проводимость участка магнитопровода, Г.

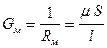. (116)

Если размеры магнитопровода неизменны, т. е. l = const и

S = const, то магнитная проводимость будет определяться магнитной проницаемостью материала участка, т. е. 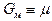. Но так как, следовательно .

Отсюда следует, что магнитное сопротивление и магнитная проводимость являются сложной нелинейной функцией индукции. Зависимость относительной магнитной проницаемости , а, следовательно, и магнитной проводимости, от величины напряженности для магнитного материала имеет вид, показанный на рис. 51.

Рис. 51. Зависимости B=f(H) 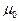– магнитная проницаемость воздуха.

и μ=f(H) Г/м.

Максимальное значение магнитной проницаемости имеет место при средних величинах индукции.

В слабых и сильных полях магнитное сопротивление материала резко возрастает. Изменение магнитного сопротивления от величины индукции сильно затрудняет решение как прямой, так и обратной задачи.

Первый закон Кирхгофа. Алгебраическая сумма магнитных потоков в узле магнитной цепи равняется нулю

. (117)

Второй закон Кирхгофа. Алгебраическая сумма падений магнитного потенциала в замкнутом контуре магнитной цепи равна алгебраической сумме МДС, действующих в этом контуре при постоянном магнитном потоке Ф = const.

ФR_м1 + ФR_м2 +...+ ФR_мi = (Iw)₁ + (Iw)₂ +...+ (Iw)_k

или

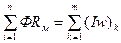. (118)