С учетом потерь в стали и короткозамкнутого витка
Для примера возьмем П-образный электромагнит переменного тока с к.з. витком на полюсе (рис. 65). Здесь S1 – площадь полюса, не охваченная экраном, S2 – экранированная площадь полюса.
Магнитный поток 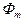 , проходя в воздушный зазор, разветвляется на два потока, один из которых Ф1 проходит через неохваченную экраном часть полюса, а другой Ф20 проходит через экран и наводит в нем ЭДС. Возникающий при этом в экране ток создает в экранированной части
, проходя в воздушный зазор, разветвляется на два потока, один из которых Ф1 проходит через неохваченную экраном часть полюса, а другой Ф20 проходит через экран и наводит в нем ЭДС. Возникающий при этом в экране ток создает в экранированной части  полюса свой магнитный поток Фэ, направленный встречно по отношению к потоку
полюса свой магнитный поток Фэ, направленный встречно по отношению к потоку 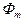 и замыкающийся через воздушный зазор и якорь. В результате совместного действия потоков Ф20 и Фэ результирующий поток Ф2 в экра-
и замыкающийся через воздушный зазор и якорь. В результате совместного действия потоков Ф20 и Фэ результирующий поток Ф2 в экра-
Рис. 66. Векторная нированной части полюса будет сдвинут по фазе
диаграмма на угол  относительно потока Ф1 в неохваченной экраном части полюса. Таким образом, в воздушном зазоре, благодаря экрану, действуют два магнитных потока, сдвинутых друг относительно друга по фазе. Это способствует устранению вибрации якоря электромагнита переменного тока. На рис. 66 приведена векторная диаграмма электромагнита с экраном.
относительно потока Ф1 в неохваченной экраном части полюса. Таким образом, в воздушном зазоре, благодаря экрану, действуют два магнитных потока, сдвинутых друг относительно друга по фазе. Это способствует устранению вибрации якоря электромагнита переменного тока. На рис. 66 приведена векторная диаграмма электромагнита с экраном.
 Составим схему замещения магнитной цепи с учетом влияния потерь в стали и экрана (рис. 67).
Составим схему замещения магнитной цепи с учетом влияния потерь в стали и экрана (рис. 67).
Решаем прямую задачу. Дано: поток в воздушном зазоре 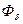 , размеры магнитной цепи и материал магнитопровода.
, размеры магнитной цепи и материал магнитопровода.
Найти намагничивающую силу катушки.
1) Известным методом определяются магнитные сопротивления (проводимости)
воздушных зазоров и проводимость рассеяния
Рис. 67. Схема замещения
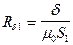 ,
, 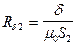 ,
, 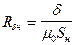 ;
; 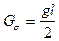 . (175)
. (175)
2) Определяется магнитное напряжение между точками ab схемы
 , (176) здесь
, (176) здесь  – индуктивное сопротивление экрана; rэ – активное сопротивление экрана;
– индуктивное сопротивление экрана; rэ – активное сопротивление экрана; 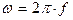 – угловая частота сети.
– угловая частота сети.
3) Индукция в якоре 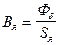 , Sя – площадь сечения якоря.
, Sя – площадь сечения якоря.
4) Магнитное сопротивление якоря. По кривой намагничивания B(H) определяется напряженность магнитного поля Hя и затем
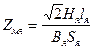 . (177)
. (177)
Если это необходимо, то можно найти также
 ,
, 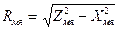 . (178)
. (178)
Здесь Pстя – потери в стали якоря; f – частота сети.
5) Магнитное напряжение в якоре
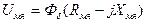 . (179)
. (179)
6) Магнитное напряжение между точками ac
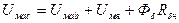 . (180)
. (180)
7) Поток рассеяния
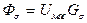 . (181)
. (181)
8) Поток в основании электромагнита
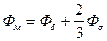 . (182)
. (182)
9) Магнитное напряжение в сердечнике
 . (183)
. (183)
10) Искомая МДС катушки
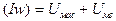 . (184)
. (184)
При решении обратной задачи необходимо задаться потоком 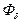 и решать методом последовательных приближений.
и решать методом последовательных приближений.
Вопросы для самоконтроля
5.8.1. Напишите формулы основных законов для магнитной цепи. Объясните каждую из входящих в формулы величин и приведите их единицы измерения.
5.8.2. Приведите кривые изменения магнитной индукции и магнитной проницаемости магнитомягкого материала в зависимости от напряженности.
5.8.3. Нарисуйте эпюру потока в сердечнике и потока рассеяния П-образного электромагнита. Изобразите кривую изменения разности магнитных потенциалов и объясните ее.
5.8.4. Напишите формулу для расчета индуктивного сопротивления обмотки электромагнита с двумя одинаковыми зазорами.
5.8.5. Приведите схему замещения магнитной цепи П-образного электромагнита постоянного тока, поясните входящие в нее сопротивления.
5.8.6. Нарисуйте векторную диаграмму электромагнита переменного тока. Объясните все входящие в них величины.
5.8.7. Нарисуйте схему замещения магнитной цепи П-образного электромагнита переменного тока с учетом потерь в стали и короткозамкнутого витка.
5.8.8. Покажите при помощи формул, что ток в катушке электромагнита переменного тока прямо пропорционален воздушному зазору.
5.8.9. Выведите выражение, описывающее изменение тока в катушке электромагнита постоянного тока при неподвижном якоре после подключения ее к источнику питания.
5.8.10. Какие процессы происходят в электромагните постоянного тока в течение времени трогания?
5.8.11. Объясните происхождение вибрации якоря в электромагнитах переменного тока.
5.8.12. Суть метода расчета магнитных проводимостей воздушных зазоров по методу Роттерса.
5.8.13. Расчет магнитной цепи электромагнита постоянного тока по методу участков.
5.8.14. В чем заключается принцип построения схем замещения магнитных цепей электромагнитов?
5.8.15. Особенности расчета магнитной цепи переменного тока.
5.9. Примеры расчета [6]
 5.9.1. Определить суммарную магнитную проводимость рабочих зазоров и удельную проводимость рассеяния прямоходового электромагнита на рис. 68.
5.9.1. Определить суммарную магнитную проводимость рабочих зазоров и удельную проводимость рассеяния прямоходового электромагнита на рис. 68.
Дано: δ = 0,1∙10-2 м;
dпн = 2,4∙10-2 м;
Рис. 68. К расчету проводимостей hпн = 0,3∙10-2 м;
прямоходового электромагнита h = 3,6∙10-2 м;
d = 1,6∙10-2 м;
Решение.Магнитная проводимость воздушного зазора [7]
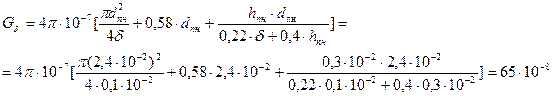 Гн.
Гн.
Суммарная магнитная проводимость двух зазоров, через которые последовательно проходит магнитный поток
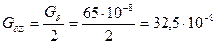 Гн.
Гн.
Удельная проводимость рассеяния по (83)
 Гн/м.
Гн/м.
5.9.2. Для электромагнита клапанного типа (рис. 69), имеющего полюсный наконечник, рассчитать магнитную проводимость рабочего и нерабочего зазоров, удельную проводимость рассеяния.
Дано: dc = 1∙10-2 м; dпн = 1,5∙10-2 м; hпн = 0,3∙10-2 м; h = 1,5∙10-2 м;
aк = 0,5∙10-2 м; δ = 0,5∙10-2 м; R0 = 2,5∙10-2 м.
Решение. Проводимость рабочего зазора

 где
где 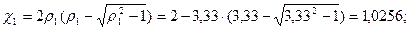
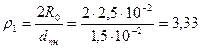 .
.
Величина нерабочего зазора зависит от рабочего. Из подобия треугольников будем иметь
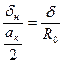 отсюда, находим
отсюда, находим
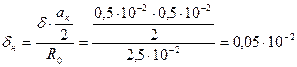 м.
м.
Рис. 69. К расчету проводимостей
Проводимость нерабочего зазора
 Гн.
Гн.
Суммарная проводимость зазоров
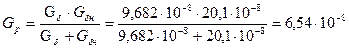 Гн.
Гн.
Проводимость рассеяния
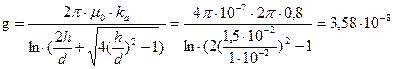 Гн/м,
Гн/м,
где 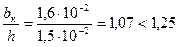 принимаем ka = 0,8.
принимаем ka = 0,8.
5.9.3. Определить поток Фδ в рабочем зазоре δ = 0,1∙10-2 м
П-образного электромагнита (рис. 70) с учетом насыщения стали и рассеяния. Удельная проводимость рассеяния gσ = 2,7∙10-6 Гн/м; суммарная проводимость рабочих зазоров GδΣ = 32,5∙10-8 Гн; МДС обмотки (Iw) = 1000 А; материал магнитопровода – сталь марки 10.
Размеры электромагнита: dпн = 2,4∙10-2 м; dc = 1,6∙10-2 м;
ая =0,6∙10-2 м; ао = 1∙10-2 м; bя = bс = 2,4∙10-2 м; h = 3,6∙10-2 м;
hпн = 0,3∙10-2 м; l = 5∙10-2 м.
Решение.Разобъем длину сердечника на две равные части
 l1=l2=0,5∙l=0,5∙5∙10-2=2,5∙10-2 м
l1=l2=0,5∙l=0,5∙5∙10-2=2,5∙10-2 м
и используем схему замещения, приведенную на рис. 71.
Без учета насыщения стали и рассеяния находим приближенно поток
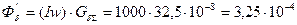 Вб.
Вб.
С учетом названных факторов поток будет меньше. Задаемся потоком первого приближения
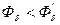 .
.
Рис. 70. П-образный электромагнит Принимая 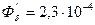 Вб, получим
Вб, получим
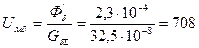 А.
А.
Индукция в якоре
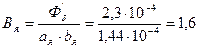 Тл.
Тл.
По кривой намагничивания стали [6] находим Hя = 25∙102 А/м и, определив lя = h + aя = 3,6∙10-2 + 0,6∙10-2 = 4,2∙10-2 м, находим

 А.
А.
Аналогично для полюсного наконечника:
 Тл;
Тл; 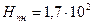 А/м;
А/м;
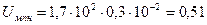 А.
А.
Между точками 1–1’ разность магнитных потенциалов будет равна: 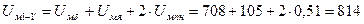 А.
А.
Поток рассеяния
 Вб, где
Вб, где 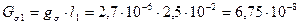 Гн.
Гн.
Поток первого участка
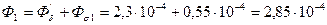 Вб.
Вб.
Индукция на первом участке
Рис. 71. Схема замещения 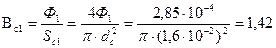 Тл.
Тл.
Напряженность поля и разность магнитных потенциалов на первом участке  А/м;
А/м;  А.
А.
Разность магнитных потенциалов между точками 2–2’ по формуле
 А,
А,
где 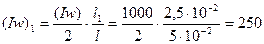 А – МДС катушки электромагнита, распределенная по длине первого участка.
А – МДС катушки электромагнита, распределенная по длине первого участка.
Аналогично произведем расчет для второго участка:
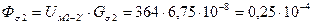 Вб,
Вб,
где 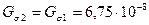 Гн.
Гн.
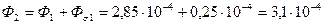 Вб;
Вб;
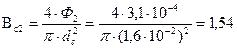 Тл;
Тл;  А/м;
А/м;
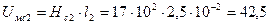 А.
А.
Для основания:
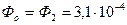 Вб;
Вб; 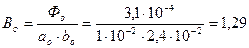 Тл;
Тл; 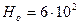 А/м;
А/м;
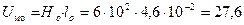 А,
А,
где 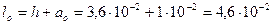 м.
м.
Суммарная МДС равна

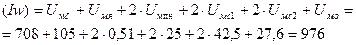 А.
А.
 Отсюда видно, что принятое значение потока Фδ достаточно близко соответсвует заданной МДС (Iw) = 1000 А, следовательно второго приближения не требуется.
Отсюда видно, что принятое значение потока Фδ достаточно близко соответсвует заданной МДС (Iw) = 1000 А, следовательно второго приближения не требуется.
5.9.4. Рассчитать магнитную цепь электромагнита переменного тока (рис. 72) без учета влияния стали и короткозамкнутого экрана.
Рис. 72. Электромагнит переменного тока
Дано:  Гн – магнитная проводимость зазора над сердечником;
Гн – магнитная проводимость зазора над сердечником;  Гн – магнитная проводимость зазора над ярмом;
Гн – магнитная проводимость зазора над ярмом;
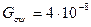 Гн – проводимость рассеяния;
Гн – проводимость рассеяния; 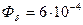 Вб – магнитный поток в среднем зазоре.
Вб – магнитный поток в среднем зазоре.
Решение.Составим полную схему замещения электромагнита, изображенного на рис. 73, а.Поскольку электромагнит симметричный относительно сердечника, то схему замещения можно упростить,
сложив ее относительно оси симметрии, как показано на рис. 73, b.
Определим результирующую проводимость зазоров, Гн

 .
.
МДС катушки электромагнита
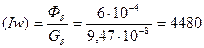 А.
А.
Рис. 73. Расчетные схемы замещения Коэффициент рассеяния
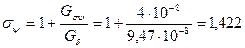 .
.
Поток рассеяния 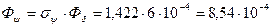 Вб.
Вб.
Магнитная проводимость магнитной цепи
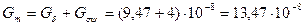 Гн.
Гн.
 5.9.5. Найти амплитудное значение магнитных потоков в якоре (Фδ), в основании (Фо) и в сердечнике (Фс) для магнитной цепи электромагнита переменного тока (рис. 74) при притянутом якоре без учета магнитного сопротивления стали.
5.9.5. Найти амплитудное значение магнитных потоков в якоре (Фδ), в основании (Фо) и в сердечнике (Фс) для магнитной цепи электромагнита переменного тока (рис. 74) при притянутом якоре без учета магнитного сопротивления стали.
Дано: U = 127 В – напряжение питания обмотки; f = 50 Гц – частота сети; w – число витков обмотки; Rδн = Rδ1 = 66,2 Гн-1; Rδ2 = 28,4 Гн-1; Rσ = 11,2 Гн-1; Xэ = 52,3 Гн-1 – магнитные проводимости воздушных зазоров;
Рис. 74. Электромагнит L = 52∙10-3, м; а = 12∙10-3, м; H = 20∙10-3, м.
переменного тока Решение.Средний магнитный поток по длине сердечника
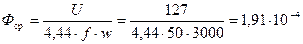 Вб.
Вб.
Поток в якоре Фδ и в основании Фо связаны с потоком Фср коэффициентами рассеяния, которые в общем случае являются комплексными величинами, но мнимой частью (вследствие ее малого значения) можно пренебречь. Коэффициенты рассеяния:
средний 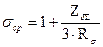 , в основании
, в основании 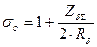 .
.
Из схемы замещения, приведенной на рис. 75 найдем

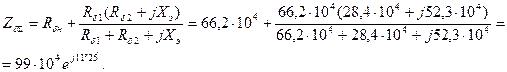
 Здесь φ = 11о25’ – угол потерь.
Здесь φ = 11о25’ – угол потерь.
Подставив значение 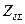 в выражения для
в выражения для 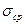 и
и  , получим
, получим
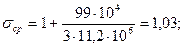
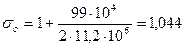 .
.
Определим искомые магнитные Рис. 75. Схема замещения без учета Zст потоки
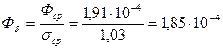 Вб,
Вб,
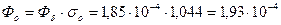 Вб.
Вб.
5.9.6. Для электромагнита, изображенного на рис. 74, составить схему замещения магнитной цепи с учетом магнитного сопротивления магнитопровода. Определить МДС и ток обмотки при притянутом якоре. Размеры магнитопровода, выполненного из стали 1212, 
значения магнитных потоков и магнитногосопротивления 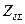 – взять из примера 5.9.5. Коэффициент заполнения стали кзс = 0,9.
– взять из примера 5.9.5. Коэффициент заполнения стали кзс = 0,9.
Решение.Схема замещения с учетом магнитных сопротивлений стальных участков:
якоря (Zя), сердечника (Zc) и основания (Zо) –
Рис. 76. Схема замещения ЭМ представлена на рис. 76.
с учетом стали Сопротивление Zя находим по потоку Фδ, Zc – по среднему потоку Фср, Zо – по потоку Фо.
Площади сечения
Sя = Sс = Sо = a∙b∙кзс = 12∙10-3∙20∙10-3∙0,9 = 2,16∙10-4 м2.
Средняя длина сердечника
lс = L – 0,5∙a = 52∙10-3 – 0,5∙12∙10-3 = 46∙10-3 м.
Средняя длина якоря и основания
lя = lо = H + a = 20∙10-3 + 12∙10-3 = 32∙10-3 м.
Определим удельные сопротивления  и
и 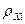 по соответствующим значениям индукции
по соответствующим значениям индукции 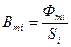 с помощью графиков зависимостей
с помощью графиков зависимостей
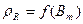 и
и 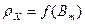 [6] для стали 1212.
[6] для стали 1212.
Расчеты  и
и 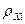 сведем в таблицу 11.
сведем в таблицу 11.
Таблица 11. Расчет значений удельных сопротивлений  и
и 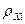 .
.
| Участок | Фmi, 10-4 Вб | Si, м2 | Bmi, Тл |  102 м/Гн
102 м/Гн
| 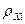 102 м/Гн
102 м/Гн
|
| Якорь | 1,85 | 2,16 | 0,856 | 2,4 | 1,0 |
| Сердечник | 1,91 | 2,16 | 0,884 | 2,4 | 1,0 |
| Основание | 1,93 | 2,16 | 0,894 | 2,5 | 1,0 |
Магнитные сопротивления
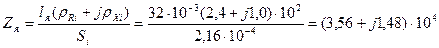 Гн-1,
Гн-1,
 Гн-1,
Гн-1,
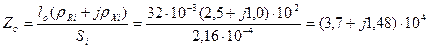 Гн-1.
Гн-1.
При определении МДС обмотки с учетом сопротивления стали фазовым сдвигом между потоками Фδ, Фср и Фо пренебрегаем. Тогда,
 Здесь
Здесь  – угол сдвига между потоком и МДС.
– угол сдвига между потоком и МДС.
Ток в обмотке электромагнита
 А.
А.
Дата добавления: 2020-10-01; просмотров: 655;











