Схемы замещения магнитной цепи.
Для удобства расчета магнитную цепь заменяют эквивалентной электрической цепью.
Таблица 10. Эквивалентные величины
| Магнитная цепь | Электрическая цепь | ||
| Обозначения | Размерность | Обозначения | Размерность |
| Магн. поток Ф | Вб= В∙ с | Ток I | А |
| МДС Iw | А | Э.д.с Е | В |
| Магн. напряж. Um | А | Электр. напряж.U | B |
| Магн. сопрот. Rm | А/В∙ с=1/Г | Электр. сопрот. R | Ом |
| Магн. провод. Gm | Г | Электр. провод.G | 1/Ом |
В электрической схеме замещения МДС заменяется ЭДС, магнитный поток – электрическим током, магнитные сопротивления – электрическими сопротивлениями. Эквивалентные величины в электрической и магнитной цепях приведены в таблице 10.
Прнцип составления схемы замещения магнитной цепи. Магнитная цепь условно разбивается на участки с равномерным сечением и постоянной магнитной проницаемостью. Затем каждый участок магнитной цепи заменяется элементом электрической цепи, а распределенная на участке МДС заменяется источником ЭДС. Так, например, схемы замещения магнитных цепей изображенных на рис. 48, а и рис. 49, а будут иметь вид, показанный на рис. 52:
 |
Рис. 52. Схемы замещения магнитных цепей
5.4. Расчет магнитных проводимостей воздушных зазоров.
При расчете магнитной цепи и определении тяговой характеристики электромагнита необходимо знать магнитную проводимость рабочего воздушного зазора и проводимости потоков рассеяния. Величина магнитной проводимости определяется конфигурацией поверхностей полюсов, ограничивающих воздушный зазор, их размерами и величиной воздушного зазора.
Существуют несколько методов расчета магнитных проводимостей: аналитический метод, метод вероятного пути потока (метод Роттерса), метод расчетных полюсов и метод построения картины поля. Рассмотрим более подробно лишь два из этих методов, а именно аналитический и метод Роттерса.
5.4.1. Аналитический метод. Если линии магнитного поля в воздушном зазоре параллельны, а эквипотенциальные поверхности представляют собой параллельные плоскости, то магнитная проводимость определяется по формуле
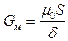 , (119)
, (119)
где S – площадь поверхности полюса, ограничивающей воздушный зазор; 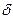 – величина воздушного зазора;
– величина воздушного зазора; 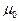 – магнитная проницаемость воздуха.
– магнитная проницаемость воздуха.
Для полюсов простой конфигурации, как например, на рис. 53, с размерами полюсов а х b магнитная проводимость будет равна
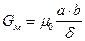 , (120)
, (120)
для полюсов цилиндрической формы с диаметром d
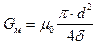 . (121)
. (121)
Однако, даже для таких простых конфигураций полюсов из-за существования поперечных сил в магнитном поле, линии магнитной индукции стремятся занять, возможно, больший объем, выпу  чиваясь по краям полюсов, образу-
чиваясь по краям полюсов, образу-
а б ющих воздушный зазор. Выпучивание
Рис. 53. Формы полюсов искажает поле и делает его неравномерным вблизи краев. Поэтому, фактически магнитное поле в зазоре является неравномерным и вышеприведенные формулы для расчета проводимостей весьма не точны. Практически этими формулами можно пользоваться для определения всей проводимости между полюсами плоской формы, если размеры a, b и d значительно больше 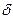 , т.е.
, т.е.
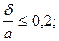

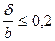 ;
; 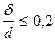 .
.
При относительно простых формах полюсов выпучивание можно учесть поправочным коэффициентом. Например, если проводимость между полюсами, изображенными на рис. 53,а, определяется по формуле
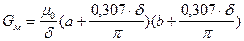 Г , (122)
Г , (122)
то поправочный коэффициент 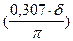 учитывает выпучивание магнитных силовых линий в зазоре. Формулы для расчета проводимостей зазоров между другими конфигурациями полюсов приводятся в справочной литературе.
учитывает выпучивание магнитных силовых линий в зазоре. Формулы для расчета проводимостей зазоров между другими конфигурациями полюсов приводятся в справочной литературе.
5.4.2.Метод вероятного пути потока или метод Роттерса.
Сущность этого метода заключается в том, что поле в воздушном зазоре разбивается на элементарные трубки, имеющие форму простых геометрических фигур, для которых легко определить площадь и магнитную проводимость. Полная проводимость между полюсами  рас-читывается как сумма проводимос-
рас-читывается как сумма проводимос-
Рис. 54. Картина поля в зазоре тей всех элементарных трубок (геометрических фигур), на которые разбито магнитное поле в зазоре. Например, поле между полюсом А (рис. 54) прямоугольной формы и плоскостью B,причем площадь плоскости B много больше площади торца полюса A, может быть представлено как сумма простых фигур: параллелепипеда 1 с площадью основания a ∙ b и высотой 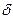 ; четырех четвертей круглого цилиндра 2 с радиусом основания
; четырех четвертей круглого цилиндра 2 с радиусом основания 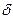 и длиной образующих a и b; четырех четвертей полого цилиндра 3 с нутренним радиусом
и длиной образующих a и b; четырех четвертей полого цилиндра 3 с нутренним радиусом 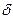 , толщиной m = (1…2)
, толщиной m = (1…2) 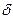 и длиной образующих a и b; четырех половин шарового квадранта 4 радиусом
и длиной образующих a и b; четырех половин шарового квадранта 4 радиусом 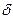 ; четырех половин квадранта шаровой оболочки 5 толщиной m и внутренним радиусом
; четырех половин квадранта шаровой оболочки 5 толщиной m и внутренним радиусом 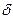 (рис. 55). Проводимость фигуры 1 и фигуры 2
(рис. 55). Проводимость фигуры 1 и фигуры 2
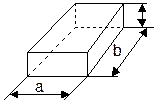
|
|
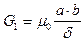
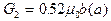
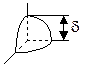
|
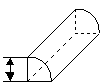
 фигуры 3 фигуры 4
фигуры 3 фигуры 4
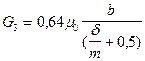
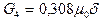

фигуры 5
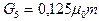 .
.
Рис. 55. Формы элементарных трубок проводимости и
формулы для их расчета
Результирующая проводимость
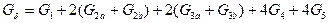 . (123)
. (123)
Магнитная проводимость рассеяния зависит от конфигурации магнитной цепи и взаимного расположения ее элементов. Так, для наиболее распространенных форм электромагнитов удельную проводимость рассеяния можно рассчитать по следующим формулам.
Для электромагнита по рис. 56, а
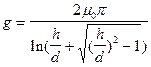 . (124)
. (124)
Для электромагнита по рис. 56, б

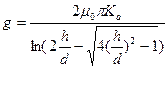 , (125) где Ка = 0,85…0,92 при
, (125) где Ка = 0,85…0,92 при
b = (1,25…2,5)h.
Для электромагнита по рис. 56, в
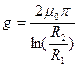 . (126)
. (126)
а б в
Рис. 56. Конструктивные формы Геометрическая проводимость
электромагнитов рассеяния 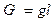 . (127)
. (127)
Приведенная проводимость рассеяния 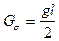 . (128)
. (128)
Коэффициент рассеяния
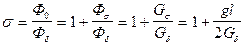 . (129)
. (129)
Дата добавления: 2020-10-01; просмотров: 607;











