Общее уравнение Шредингера. Модели строения атомов. Энергетические уровни свободных атомов
65. Вероятность нахождения частицы в объеме 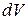 :
:
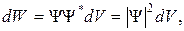
где 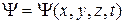 – волновая функция, описывающая состояние частицы;
– волновая функция, описывающая состояние частицы; 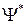 –функция, комплексно сопряженная с
–функция, комплексно сопряженная с 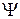 ;
; 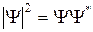 – квадрат модуля волновой функции.
– квадрат модуля волновой функции.
66. Для стационарных состояний:
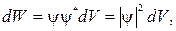
где 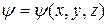 – координатная (амплитудная) часть волновой функции.
– координатная (амплитудная) часть волновой функции.
67. Условие нормировки вероятностей:
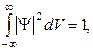
где интегрирование производится по всему бесконечному пространству, т.е. по координатам x,y,z от 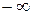 до
до 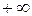 .
.
68. Вероятность обнаружения частицы в интервале от х 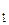 до х2:
до х2:
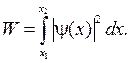
69. Среднее значение физической величины L, характеризующей частицу, находящуюся в состоянии, описываемом волновой функцией 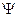 :
:
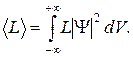
70. Общее уравнение Шредингера (уравнение Шредингера, зависящее от времени):
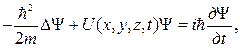
где 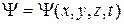 –волновая функция, описывающая состояние частицы;
–волновая функция, описывающая состояние частицы; 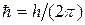 ; m – масса частицы;
; m – масса частицы; 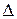 – оператор Лапласа
– оператор Лапласа 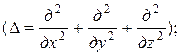
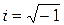 – мнимая единица;
– мнимая единица; 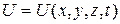 – потенциальная энергия частицы в силовом поле, в котором она движется.
– потенциальная энергия частицы в силовом поле, в котором она движется.
71. Уравнение Шредингера для стационарных состояний:
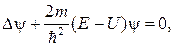
где 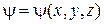 – координатная часть волновой функции
– координатная часть волновой функции 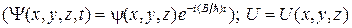 – потенциальная энергия частицы; E – полная энергия частицы.
– потенциальная энергия частицы; E – полная энергия частицы.
72. Волновая функция, описывающая одномерное движение свободной частицы:
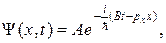
где А – амплитуда волн де Бройля; 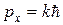 –импульс частицы;
–импульс частицы; 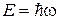 – энергия частицы.
– энергия частицы.
73. Собственные значения энергии 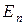 частицы, находящейся на n-м энергетическом уровне в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»:
частицы, находящейся на n-м энергетическом уровне в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»:
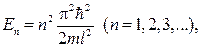 ,
,
где l – ширина ямы.
74. Собственная волновая функция, соответствующая вышеприведенному собственному значению энергии:
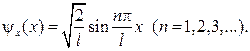
75. Коэффициент прозрачности D прямоугольного потенциального барьера конечной ширины:
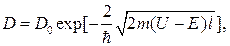
где D 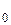 – множитель, который можно приравнять единице; U – высота потенциального барьера; Е – энергия частицы.
– множитель, который можно приравнять единице; U – высота потенциального барьера; Е – энергия частицы.
76. Уравнение Шредингера для линейного гармонического осциллятора в квантовой механике:
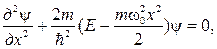
где 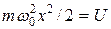 – потенциальная энергия осциллятора;
– потенциальная энергия осциллятора; 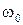 – собственная частота колебаний осциллятора; m – масса частицы.
– собственная частота колебаний осциллятора; m – масса частицы.
77. Собственные значения энергии гармонического осциллятора:
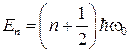
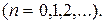
78. Энергия нулевых колебаний гармонического осциллятора:
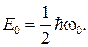
79. Потенциальная энергия U(r) взаимодействия электрона с ядром в водородоподобном атоме:
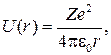
где r – расстояние между электроном и ядром; Z – порядковый номер элемента; 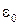 – электрическая постоянная.
– электрическая постоянная.
80. Собственное значение энергии 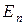 электрона в водородоподобном атоме:
электрона в водородоподобном атоме:
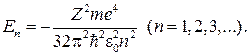
81. Энергия ионизации атома водорода:
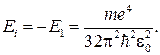
82. Момент импульса (механический орбитальный момент) электрона:
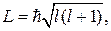
где l – орбитальное квантовое число, принимающие при заданном n следующие значения: 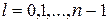 (всего n значений).
(всего n значений).
83. Проекция момента импульса на направление z внешнего магнитного поля:
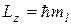 ,
,
где m 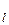 – магнитное квантовое число, принимающее при заданном l следующие значения:
– магнитное квантовое число, принимающее при заданном l следующие значения: 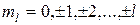 (всего (2l+1) значений).
(всего (2l+1) значений).
84. Правила отбора для орбитального и магнитного квантовых чисел:
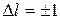 и
и 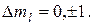
85. Спин (собственный механический момент импульса) электрона:
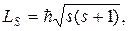
где s – спиновое квантовое число (s=1/2).
86. Проекция спина на направление z внешнего магнитного поля:
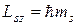 ,
,
где 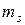 – магнитное спиновое квантовое число (m
– магнитное спиновое квантовое число (m  =
= 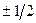 ).
).
87. Принцип Паули:
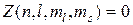 или 1,
или 1,
где 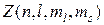 – число электронов, находящихся в квантовом состоянии, описываемом набором четырех квантовых чисел: n – главного, l – орбитального, m
– число электронов, находящихся в квантовом состоянии, описываемом набором четырех квантовых чисел: n – главного, l – орбитального, m  – магнитного спинового, m
– магнитного спинового, m 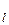 – магнитного.
– магнитного.
88. Максимальное число электронов Z(n), находящихся в состояниях, определяемых данным главным квантовым числом n:
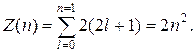
89. Коротковолновая граница сплошного рентгеновского спектра:
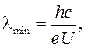
где e – заряд электрона, U – разность потенциалов, приложенная к рентгеновской трубке.
90. Закон Мозли, определяющий частоты спектральных линий характеристического рентгеновского излучения:
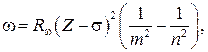
где R – постоянная Ридберга; Z – порядковый номер элемента в периодической системе; 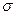 –постоянная экранирования; т определяет рентгеновскую серию (т=1,2,3,...); n определяет отдельные линии соответствующей серии (n=m+1,m+2,...).
–постоянная экранирования; т определяет рентгеновскую серию (т=1,2,3,...); n определяет отдельные линии соответствующей серии (n=m+1,m+2,...).
91. Закон Мозли для линии 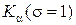 :
:
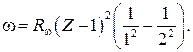
Дата добавления: 2016-07-22; просмотров: 1625;











