Пример решения задач на определение линейной плотности заряда на стержне
Пример 1. Тонкий стержень длиной 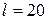 см несет равномерно распределенный заряд. На продолжении оси стержня на расстоянии
см несет равномерно распределенный заряд. На продолжении оси стержня на расстоянии
а = 10 см от ближайшего конца находится точечный заряд 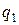 = 40 нКл, который взаимодействует со стержнем с силой F = 6мкН. Определить линейную плотность
= 40 нКл, который взаимодействует со стержнем с силой F = 6мкН. Определить линейную плотность 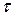 заряда на стержне.
заряда на стержне.
РЕШЕНИЕ. Сила взаимодействия F заряженного стержня с точечным зарядом 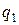 зависит от линейной плотности
зависит от линейной плотности 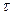 заряда на стержне. Зная эту зависимость, можно определить
заряда на стержне. Зная эту зависимость, можно определить 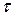 . При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим на стержне малый участок
. При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим на стержне малый участок 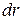 сзарядом
сзарядом 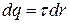 . Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона:
. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона:
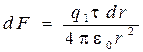 .
.
Интегрируя это выражение в пределах от а до 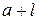 , получим:
, получим:
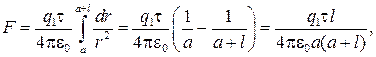
откуда интересующая нас линейная плотность заряда
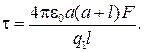
Выразим все величины в единицах СИ: 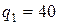 нКл =
нКл = 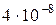 Кл,
Кл, 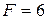 мкН =
мкН = 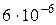 Н,
Н, 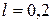 м,
м, 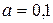 м,
м, 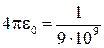 .
. 
Подставим числовые значения величин в полученную формулу и произведем вычисления:
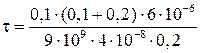 Кл/м =
Кл/м = 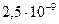 Кл/м =
Кл/м = 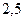 нКл/м.
нКл/м.
Пример 2. Определить внутреннее сопротивление источника тока, если во внешней цепи при силе тока 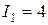 А развивается мощность
А развивается мощность 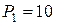 Вт, а при силе тока I2= 6 А – мощность
Вт, а при силе тока I2= 6 А – мощность 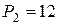 Вт.
Вт.
РЕШЕНИЕ. Мощность, развиваемая током:
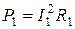 и
и 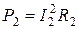 , (1)
, (1)
где 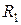 и
и 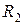 –сопротивление внешней цепи.
–сопротивление внешней цепи.
Согласно закону Ома:
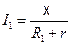 ;
; 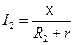 ,
,
где 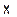 – э.д.с. источника. Решив этих два уравнения относительно r, получим:
– э.д.с. источника. Решив этих два уравнения относительно r, получим:
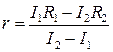 . (2)
. (2)
Выразив 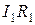 и
и 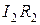 и подставив в выражение (2), найдем искомое внутреннее сопротивление источника тока:
и подставив в выражение (2), найдем искомое внутреннее сопротивление источника тока:
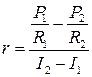 .
.
Вычисляя, получаем: 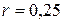 Ом.
Ом.
Пример 3. Электрон, влетев в однородное магнитное поле с магнитной индукцией 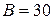 мТл, движется по окружности радиусом
мТл, движется по окружности радиусом 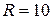 см. Определить магнитный момент
см. Определить магнитный момент 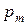 эквивалентного кругового тока.
эквивалентного кругового тока.
РЕШЕНИЕ. Так как движение электрона по окружности эквивалентно круговому току, то магнитный момент кругового тока:
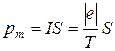 , (1)
, (1)
где е – заряд электрона, Т – период обращения электрона; S – площадь, ограниченная окружностью, описываемой электроном;

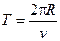 (v – скорость электрона);
(v – скорость электрона); 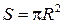 .
.
Согласно второму закону Ньютона:
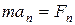 ; или
; или 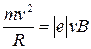 (2)
(2)
(сила Лоренца перпендикулярна вектору скорости и сообщает электрону нормальное ускорение). Из выражения (2) получим, что скорость
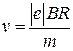 .
.
Тогда
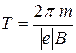 .
.
Подставив выражения для 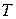 и
и 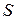 в формулу (1), получим искомый магнитный момент эквивалентного кругового тока:
в формулу (1), получим искомый магнитный момент эквивалентного кругового тока:
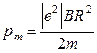 .
.
Вычисляя, получим 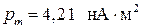 .
.
Пример 4.Светильник в виде равномерно светящегося шара в 500 кд имеет диаметр 50 см. Определить: полный световой поток F, излучаемый светильником; его светимость R; освещенность Е, светимость R1и яркость В1экрана, на который падает 20% светового потока, излучаемого светильником. Площадь экрана составляет 0,5 м2, а коэффициент отражения света его поверхностью 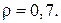
РЕШЕНИЕ. Полный световой поток, испускаемый изотропным точечным источником:
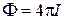 .
.
Светимость источника света:
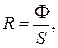
где S – площадь поверхности светильника: 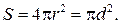
Тогда
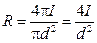 .
.
Так как по условию на экран падает световой поток 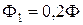 , то освещенность экрана:
, то освещенность экрана:
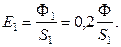
Светимость экрана:
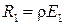 .
.
Яркость экрана:
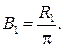
Вычисляя, получаем:1) F= 6,28 клм; 2) R = 8 клм/м2;
3) Е 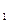 = 2,51 клк; R
= 2,51 клк; R 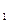 = 1,76 клм/м2; B
= 1,76 клм/м2; B 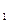 =560 кд/м2.
=560 кд/м2.
Пример 5. Плосковыпуклая линза (n= 1,6) выпуклой стороной прижата к стеклянной пластинке. Расстояние между первыми двумя кольцами Ньютона, наблюдаемыми в отраженном свете, равно 0,5 мм. Определить оптическую силу линзы, если освещение производится монохроматическим светом с 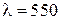 нм, падающим нормально.
нм, падающим нормально.
РЕШЕНИЕ. Оптическая сила линзы в общем случае:
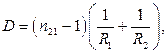
где 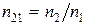 – относительный показатель преломления (n
– относительный показатель преломления (n 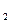 и n
и n 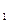 соответственно показатели преломления линзы и окружающей среды); R
соответственно показатели преломления линзы и окружающей среды); R 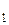 и R
и R 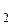 – радиусы кривизны поверхностей линзы.
– радиусы кривизны поверхностей линзы.
Поскольку линза – плосковыпуклая и находится в воздухе, для нее оптическая сила:
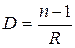 . (1)
. (1)
Для определения радиуса линзы воспользуемся выражением для радиуса темного кольца Ньютона в отраженном свете:
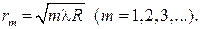
Разность радиусов первых двух темных колец:
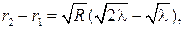
откуда
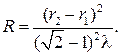 (2)
(2)
Подставив (2) в (1), найдем искомую оптическую силу линзы:
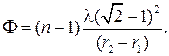
Вычисляя, получим:
F=0,547 дптр.
Пример 6. Давление монохроматического света с длиной волны 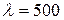 нм на поверхность с коэффициентом отражения
нм на поверхность с коэффициентом отражения 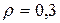 , расположенную перпендикулярно падающему свету, равно 0,2 мкПа. Определить число фотонов, падающих ежесекундно на единицу площади этой поверхности.
, расположенную перпендикулярно падающему свету, равно 0,2 мкПа. Определить число фотонов, падающих ежесекундно на единицу площади этой поверхности.
РЕШЕНИЕ. Давление, производимое светом при нормальном падении на поверхность:
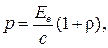
где Ее – облученность поверхности, т.е. энергия всех фотонов, падающих в единицу времени на единицу поверхности; 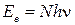 .
.
Так как 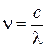 , то
, то 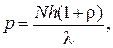
откуда искомое число фотонов, падающих ежесекундно на единицу площади поверхности:
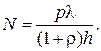
Вычисляя, получаем:
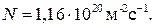
Пример 7. Определить частоту света, излучаемого возбужденным атомом водорода, при переходе электрона на второй энергетический уровень, если радиус орбиты электрона изменился в 9 раз.
РЕШЕНИЕ. Согласно обобщенной формуле Бальмера, частота света, излучаемого атомом водорода:
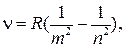 (1)
(1)
где 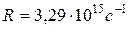 – постоянная Ридберга; т – определяет серию (по условию задачи, т = 2 – серия Бальмера), т.е. номер орбиты, на который переходит электрон; п определяет отдельную линию серии, т.е. номер орбиты, с которой переходит электрон.
– постоянная Ридберга; т – определяет серию (по условию задачи, т = 2 – серия Бальмера), т.е. номер орбиты, на который переходит электрон; п определяет отдельную линию серии, т.е. номер орбиты, с которой переходит электрон.
Второй закон Ньютона для электрона, движущегося по окружности радиусом r 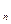 под действием кулоновской силы:
под действием кулоновской силы:
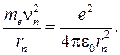 (2)
(2)
Согласно теории Бора, момент импульса электрона, движущегося по n-ой орбите:
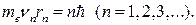 (3)
(3)
Решая уравнения (2) и (3), получим:
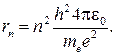 (4)
(4)
Из выражения (4) и условия задачи следует, что
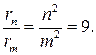 (5)
(5)
Умножив и разделив правую часть уравнения (1) на m 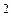 и учитывая (5), получим искомую частоту:
и учитывая (5), получим искомую частоту:
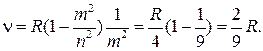
Вычисляя, получаем:
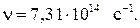
Дата добавления: 2016-07-22; просмотров: 4362;











