Понятие о спектре периодических и непериодических сигналов

Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции. Значение гармонических сигналов обусловлено рядом причин:

I.Гармонические сигналы инварианты относительно преобразований, осуществляемых стационарными линейными электрическими цепями. Если такая цепь возбуждена источником гармонических колебаний, то сигнал на выходе цепи остаётся гармоническим с той же частотой, отличаясь от входного сигнала лишь амплитудой и начальной фазой.

II.Техника генерирования гармонических сигналов относительна проста. Будем использовать гармонические сигналы в качестве ортонормированного базиса.

Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, т.е. разложен по частоте, то говорят, что осуществлено спектральное разложение сигнала.

Совокупность значений амплитуд и фаз гармонических компонент на различных частотах называется спектром сигнала.

2.2 Спектральное представление периодических сигналов

Математической моделью процесса, повторяющегося во времени, является периодический сигнал 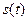со следующим свойством:

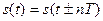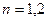, , (2.1)

где Т- период сигнала.

Найдём спектральное разложение такого сигнала.

В соответствии с формулой (1.10) получим спектральное разложение:

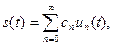(2.2)

справедливое на всей бесконечности оси времени.

Ряд вида (2.2) называется рядом Фурье данного сигнала.

Введём понятия основной частоты 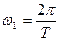последовательности, образующей периодический сигнал. Примем интервал разложения от 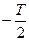до 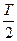. Вычисляя коэффициенты разложения по формуле (1.12) запишем ряд Фурье для периодического сигнала:

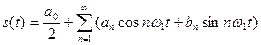(2.3)

с коэффициентами:

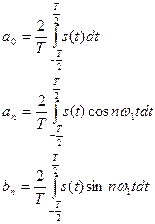(2.4)

В общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами 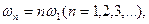кратными основной частоте последовательности.

Каждую гармонику можно описать её амплитудой 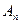и начальной фазой 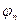. Для этого коэффициенты ряда Фурье записывают в виде:

, ,

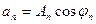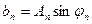так что:

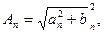
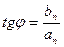
Подставив эти выражения в (2.3), получим другую, эквивалентную форму ряда Фурье:

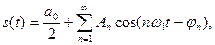(2.5)

которая иногда оказывается удобнее.

Изобразим коэффициенты ряда Фурье графически. Такое изображение называется спектральной диаграммой сигнала.

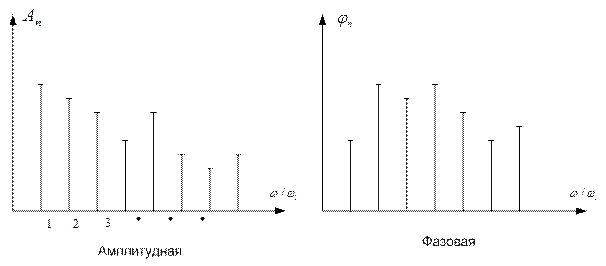
Спектры периодических сигналов являются дискретными. Спектральное разложение можно выполнить также, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:

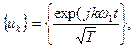
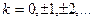(2.6)

Функции этой системы периодичны с периодом Т и ортонормированны на отрезке времени .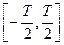

Тогда мы получим показательную форму записи ряда Фурье:

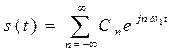(2.7)

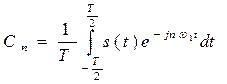
(2.8)

Выражение (2.7) представляет собой ряд Фурье в комплексной форме.

Спектр сигнала в соответствии с формулой (2.8) содержит компоненты на отрицательной полуоси частот, причём 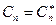. Слагаемые в ряде (2.7) с положительными и отрицательными частотами объединяются в пары.

Отрицательная частота – понятие не физическое, а математическое, вытекающее из способа представления комплексных чисел.