Некоторые элементы функционального анализа сигналов
В основе функционального анализа сигналов лежит (представление) сигнала как вектора, в специальным образом сконструированном бесконечномерном пространстве.
Пусть 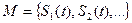 - множество сигналов. Причина объединения этих объектов – наличие некоторых свойств, общих для всех элементов множества
- множество сигналов. Причина объединения этих объектов – наличие некоторых свойств, общих для всех элементов множества 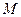 .
.
Исследование свойств сигналов, образующих такие множества, можно осуществлять , если выражать одни элементы множества через другие элементы. При этом считается, что множество сигналов наделено определённой структурой. Электрические колебания могут складываться, а также умножаться на произвольный масштабный коэффициент. Это даёт возможность в множествах сигналов ввести структуру линейного пространства.
Множество сигналов 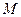 образует вещественное линейное пространство, если справедливы следующие аксиомы:
образует вещественное линейное пространство, если справедливы следующие аксиомы:
1. Любой сигнал 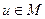 при любых
при любых 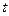 принимает лишь вещественные значения.
принимает лишь вещественные значения.
2. Для любых 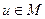 и
и 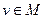 существует их сумма
существует их сумма 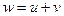 , причём
, причём 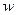 также содержится в
также содержится в 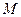 . Операция суммирования коммутативна:
. Операция суммирования коммутативна: 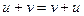 и ассоциативна
и ассоциативна 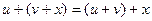 .
.
3. Для любого сигнала 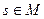 и любого вещественного числа
и любого вещественного числа 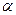 определён сигнал
определён сигнал 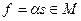 .
.
4. Множество 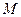 содержит особый нулевой элемент
содержит особый нулевой элемент 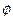 , такой, что
, такой, что 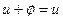 для всех
для всех 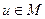 .
.
Линейное пространство, элементами которого являются функции, называется функциональным.
Если математические модели сигналов принимают комплексные значения , то, допуская в аксиоме 3 умножение на комплексное число, можем ввести понятие комплексного линейного пространства.
Как и в обычном трёхмерном пространстве в линейном пространстве сигналов можно выделить специальное подмножество, играющее роль координатных осей. В качестве таких осей используются линейно независимые векторы.
Совокупность векторов 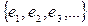 ,принадлежащих
,принадлежащих 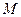 , является линейно независимой, если равенство:
, является линейно независимой, если равенство:
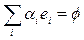 (1.1)
(1.1)
возможно лишь в случае одновременного обращения в нуль всех числовых коэффициентов 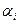 .
.
Система линейно независимых векторов образует координатный базис в линейном пространстве.
Введём новое понятие, которое по своему смыслу соответствует длине вектора. Это позволит не только определить, что один сигнал больше другого, но и указать на сколько он больше.
Длину вектора называют его нормой. Линейное пространство сигналов L является нормированным , если каждому вектору 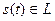 однозначно сопоставлено число
однозначно сопоставлено число 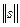 - норма этого вектора.
- норма этого вектора.
Аксиомы нормированного пространства
1. Норма неотрицательна, т.е. 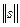
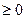 . Норма
. Норма 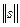 =0 тогда и только тогда, если
=0 тогда и только тогда, если 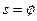
2. Для любого числа 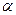 справедливо равенство
справедливо равенство 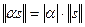 .
.
3. Если 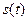 и
и 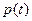 - два вектора из L, то выполняется неравенство:
- два вектора из L, то выполняется неравенство:
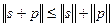
Существуют разные способы определения нормы сигналов. Чаще всего полагают, что вещественные аналоговые сигналы имеют норму:
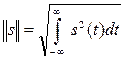 (1.2)
(1.2)
(из двух возможных значений корня выбирается положительное). Для комплексных сигналов норма:
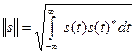 ,
,
где *-символ комплексно-сопряжённой величины.
Квадрат нормы называется энергией сигнала
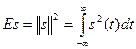 (1.3)
(1.3)
Такая энергия выделяется в резисторе с сопротивлением 1Ом, если на его зажимах существует напряжение 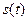 .
.
Необходимо ввести фундаментальное понятие, которое обобщало бы наше обычное представление о расстоянии между точками в пространстве.
Говорят, что линейное пространство L становится метрическим пространством, если каждой паре элементов 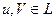 сопоставлено неотрицательное число
сопоставлено неотрицательное число 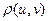 , называемое метрикой, или расстоянием между этими элементами. Метрика, независимо от способа её определения, должна подчиняться аксиомам метрического пространства:
, называемое метрикой, или расстоянием между этими элементами. Метрика, независимо от способа её определения, должна подчиняться аксиомам метрического пространства:
1.Метрика рефлексивна 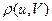 =
= 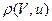
2. 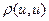 =0 при любых
=0 при любых 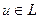 .
.
3.Каков бы ни был элемент 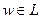 , всегда
, всегда 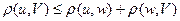 .
.
Установим взаимосвязь между нормой и метрикой. Обычно метрику определяют как норму разности двух сигналов :
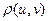 =
= 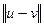 (1.4)
(1.4)
Норму в свою очередь, можно понимать как расстояние между выбранным элементом пространства и нулевым элементом: 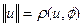 .
.
Дата добавления: 2016-07-22; просмотров: 2034;











