Тема 5.3 Подстановки. Обратные подстановки. Формула количества подстановок.
Взаимооднозначное отображение множества {1,2,3, …,n} на само себя называется подстановкой n чисел, где n – степень подстановки.
Обычно подстановку записывают в виде двух строк, заключенных в скобки. При этом в первой строке аргументы (первые координаты), а во второй строке в соответствующие им образы (вторые координаты).
Общая формула количества подстановок:
Если степень подстановки =n – то количество подстановок: n!
Из всех подстановок выделяют так называемую тождественную подстановку.

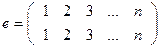
Если подстановка 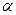 имеет вид
имеет вид 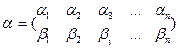 , то симметричная ей подстановка
, то симметричная ей подстановка 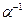 получается если поменять местами строки подстановки
получается если поменять местами строки подстановки 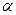
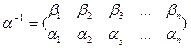
Произведением подстановок 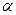 и
и 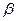 называется новая подстановка
называется новая подстановка 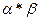 , полученная путем применения сначала подстановки
, полученная путем применения сначала подстановки 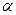 , затем подстановки
, затем подстановки 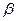 .
.
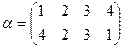
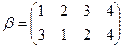
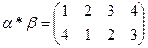
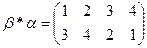
Свойства:
1. 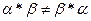 - произведение подстановок не коммутативно;
- произведение подстановок не коммутативно;
2. 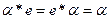
3. 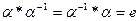
Подстановка называется четной, если общее число инверсий в ее строках, есть число четное, в противном случае подстановка называется нечетной.
Два числа образуют инверсию, если меньшее из них находиться правее большего.
Общее число инверсий определяют следующим образом:
1. определяем число инверсий для первой строки: для каждого числа подсчитываем количество чисел, меньше чем оно и стоящих правее его.
2. определяем число инверсий для второй строки: для каждого числа подсчитываем количество чисел, меньше чем оно и стоящих правее его.
3. складываем полученные значения.
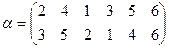
1. 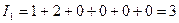
2. 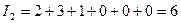
3. 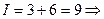 9 – нечетное, следовательно
9 – нечетное, следовательно 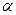 – нечетная подстановка.
– нечетная подстановка.
Циклом называется такая подстановка, каждый элемент 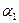 переходит в элемент
переходит в элемент 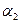 ,
, 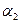 переходит в элемент
переходит в элемент 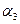 , …,
, …, 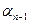 переходит в элемент
переходит в элемент 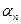 ,
, 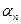 переходит в элемент
переходит в элемент 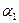
Цикл длины два называется транспозицией.
Любую подстановку можно представить в виде произведения независимых циклов.
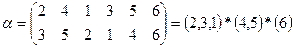
Цикл длины один разрешается опускать в разложении подстановки в виде произведений.
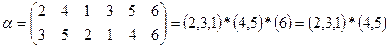
Обозначим m – число независимых циклов: m=3.
Декрементом (d) называется разность n – m, где n – степень подстановки, m – количество независимых циклов. Четность подстановки совпадает с четностью ее декремента:
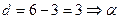 - нечетная подстановка.
- нечетная подстановка.
Методика решения уравнений с подстановками:
1. 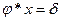 , где
, где 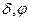 - известные подстановки, х – неизвестная подстановка.
- известные подстановки, х – неизвестная подстановка.
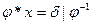
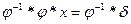
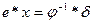
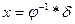
2. 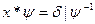 , где
, где 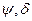 - известные подстановки, х – неизвестная подстановка
- известные подстановки, х – неизвестная подстановка
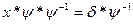
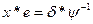
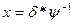
3. 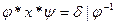
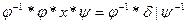
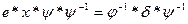
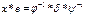
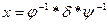
Дата добавления: 2016-07-22; просмотров: 4714;











