Тема 5.1 Отображения и их свойства.

Пусть XY – произвольные множества, если каждому элементу x из множества X (x ∈ X) ставится в соответствие элемент y ∈ Y, то говорят, что на множестве X задано отображение со значениями во множестве Y.

Пусть: X→Y либо f(x) = y.

Множество X – называется областью определения.

Множество Y – область прибытия.

Областью значений отображения f: X→Y называется множество f(X), состоящее из y ∈ Y, такого что y= f(x) для x ∈ X

f(X)={y| y ∈ Y, y= f(x), для x ∈ X }

Область значения всегда является подмножеством Y, но не всегда совпадает с ним f(X)≤Y

Существуют следующие способы задания отображений:

1. аналитический, то есть когда отображение задается в виде формулы;

2. словесный – описанием с помощью слов;

3. табличный

x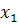
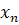
y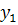

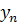
4. графический (график , диаграмма)

Свойства:

1. Отображение f: X→Y называется сюръекцией, если область прибытия совпадает с областью значений, то есть f(X)=Y или если для любого y ∈ Y J x ∈ X, такой что f(x)=y

X Y

2. Отображенное f: X→Y называется инъекцией, если для любых
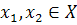, таких что 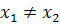выполняется что значения соответствовать этим аргументам не будут совпадать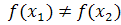

А если для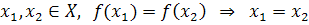

X Y X Y

не является инъекцией

Отображение f=X→Y называется биекцией, если оно является сюръекцией и инъекцией, или для любого элемента y ∈ Y существует и притом единственный x ∈ X, такой, что f(x)=y.

X Y

Биекция также называется взаимно-однозначным отображением.