Самостоятельная работа №10.
Контрольная работа
Вариант 1
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно”
Второй уровень сложности – любые четыре задачи – оценка “хорошо”
Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов:
а). « 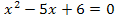 на множестве действительных чисел R »
на множестве действительных чисел R »
б). « 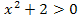 на множестве действительных чисел R »
на множестве действительных чисел R »
в). « 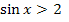 на множестве действительных чисел»
на множестве действительных чисел»
2. Дана формула 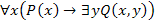 . Являются ли вхождения переменной x свободными?
. Являются ли вхождения переменной x свободными?
3. Высказывательная форма x+y=z , с переменными, упорядоченными по алфавиту и принимающими значения из множества однозначных натуральных чисел, задаёт предикат F(x,y,z) . Выпишите тройки чисел, компоненты которых находятся в отношении F.
4. Задано бинарное отношение 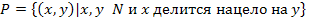 . Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
. Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
5. Пусть бинарные отношения P и S определены на М, где М-множество всех людей следующим образом:
P= {(x,y) | x,y M,x является отцом y}
S= {(x,y) | x,y M,x - дочь y}
Описать явно следующие отношения:
а). PS b) 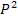 c).
c). 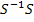 d)
d) 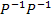
Вариант 2
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно”
Второй уровень сложности – любые четыре задачи – оценка “хорошо”
Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов:
а). « 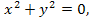 x,y
x,y 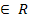 - множество действительных чисел»
- множество действительных чисел»
б). « 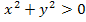 на множестве действительных чисел R »
на множестве действительных чисел R »
в). « 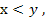 если
если 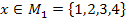 и
и 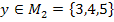 »
»
2. Дана формула 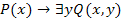 . Являются ли вхождения переменной x связанными?
. Являются ли вхождения переменной x связанными?
3. Высказывательная форма « x – среднее арифметическое y и z » , с переменными, упорядоченными по алфавиту и принимающими значения из множества однозначных натуральных чисел, задаёт предикат F(x,y,z) . Выпишите тройки чисел, компоненты которых находятся в отношении F.
4. Задано бинарное отношение 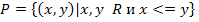 . Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
. Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
5. Пусть бинарные отношения P и S определены на М, где М-множество всех людей следующим образом:
P= {(x,y) | x,y 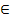 M, x является отцом y}
M, x является отцом y}
S= {(x,y) | x,y 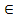 M, x - дочь y}
M, x - дочь y}
Описать явно следующие отношения:
а). 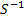 b)
b) 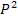 c).
c). 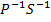 d)
d) 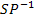
Вариант 3
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно”
Второй уровень сложности – любые четыре задачи – оценка “хорошо”
Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов:
а). « 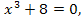 x
x 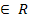 - множество действительных чисел»
- множество действительных чисел»
б). « 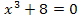 на множестве натуральных чисел N »
на множестве натуральных чисел N »
в). « 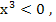 на множестве натуральных чисел N »
на множестве натуральных чисел N »
2. Дана формула 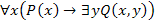 . Являются ли вхождения переменных x и y связанными?
. Являются ли вхождения переменных x и y связанными?
3. Высказывательная форма « y равен квадратному корню из произведения чисел x и z » , с переменными, упорядоченными по алфавиту и принимающими значения из множества однозначных натуральных чисел, задаёт предикат F(x,y,z) . Выпишите тройки чисел, компоненты которых находятся в отношении F.
4. Задано бинарное отношение 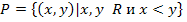 . Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
. Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
5. Пусть бинарные отношения P и S определены на М, где М-множество всех людей следующим образом:
P= {(x,y) | x,y 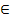 M, x является матерью y}
M, x является матерью y}
S= {(x,y) | x,y 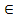 M, x - сын y}
M, x - сын y}
Описать явно следующие отношения:
а). PS b) 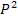 c). SP d)
c). SP d) 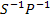
Вариант 4
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно”
Второй уровень сложности – любые четыре задачи – оценка “хорошо”
Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов:
а). « 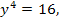 x,y
x,y 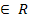 - множество действительных чисел»
- множество действительных чисел»
б). « 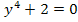 на множестве действительных чисел R »
на множестве действительных чисел R »
в). « 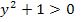 на множестве действительных чисел»
на множестве действительных чисел»
2. Дана формула 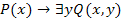 . Являются ли вхождения переменной y связанными?
. Являются ли вхождения переменной y связанными?
3. Высказывательная форма « x+y делится нацело на z » , с переменными, упорядоченными по алфавиту и принимающими значения из множества однозначных натуральных чисел, задаёт предикат F(x,y,z) . Выпишите тройки чисел, компоненты которых находятся в отношении F.
4. Задано бинарное отношение 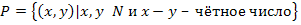 . Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
. Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
5. Пусть бинарные отношения P и S определены на М, где М-множество всех людей следующим образом:
P= {(x,y) | x,y 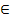 M, x является отцом y}
M, x является отцом y}
S= {(x,y) | x,y 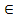 M, x - дочь y}
M, x - дочь y}
Описать явно следующие отношения:
а). 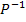 b)
b) 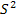 c).PS d)
c).PS d) 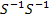
Дата добавления: 2016-07-22; просмотров: 2033;











