Тема 4.4 Понятие предикатной формулы.

Напомним некоторые из определений и введем понятие формулы логики предикатов аналогично тому, как это было сделано в логике высказываний.

Зададим сначала алфавит символов, их которых будем составлять формулы:

· предметные переменные: х, у, z, x_i, y_i,z_i (i – натуральное число);

· предикатные буквы: P, Q, R, …;

· символы операций – отрицания, конъюнкции, дизъюнкции, импликации, эквиваленции;

· кванторы общности и существования;

· вспомогательные символы – скобки, запятая.

Определение.

1. Всякий нуль-местный предикатный символ – формула.

2. Всякий n–местный предикатный символ – формула.

3. Если F – формула, а x - предметная переменная, то "x(F) и $x(F) – формулы.

4. Если F₁ и F₂ – формулы, то 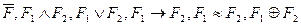- формулы.

5. Никаких других формул в логике предикатов нет.

Определение. Формулы, определенные в п. 1 и 2, называются элементарными. Формулы, не являющиеся элементарными, называют составными.

Пример

1. Р; Q(x, y, z); R(x₁, x₂) – элементарные формулы.

2. "х (Р(x, y, z); "x ($y (P(x, y, z))); 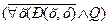- составные формулы.

Формула F в формулах вида "x(F) и $x(F) называется соответственно областью действия квантора "x или $x.

Вхождение переменной в формулу называется связанным, если оно находится в области действия квантора по этой переменной или является вхождением в этот квантор; вхождение, не являющееся связанным, называется свободным (область действия квантора всегда однозначно определяется по виду формулы).

Переменная называется свободной в формуле, если хотя бы одно ее вхождение в этой формуле свободно.

Формулы без свободных предметных переменных называются замкнутыми, а формулы, содержащие свободные переменные – открытыми.