Численное решение ДУ

Для решения дифференциальных уравнений в численном виде используется функция dsolve с параметром numeric или type=numeric. При этом решение возвращается в виде специальной процедуры, по умолчанию реализующей широко известный метод решения дифференциальных уравнений Рунге-Кутта-Фелберга порядков 4 или 5. Эта процедура называется rkf45 и символически выводится (без тела) при попытке решения заданной системы дифференциальных уравнений. Указанная процедура возвращает особый тип данных, позволяющий найти решение в любой точке или построить график решения. При этом используется функция plot[odeplot] из пакета odeplot, предназначенного для визуализации решений ДУ. Процедура имеет особый вид listprocedure и для преобразования листа выходных данных в векторы Y и Z используется функция subs.

В списке параметров функции dsolve можно явным образом включить указание на метод решения: опция method=dverk78 – задаёт решение методом Рунге – Кутта 7 и 8 порядка; опция 'abserr'=aerr – задаёт велияину абсолютной погрешности решения; опция 'minerr'=mine – задаёт минимальную величину погрешности.

Далее приведено решение системы ДУ численным методом.

> restart;

> s:=diff(y1(x),x)=2*sqrt(3*x*x+y1(x)*y1(x)+y1(x)),

diff(y2(x),x)=sqrt(x*x+y1(x)*y1(x)+y2(x));

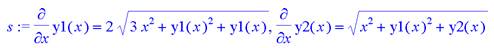
> f:={y1(x),y2(x)};

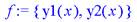
> p:=dsolve({s,y1(0)=0,y2(0)=1},f,numeric);

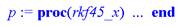
> p(2);

> plots[odeplot](p,[x,y1(x)],0..2.5,labels=[x,y1],color=black);

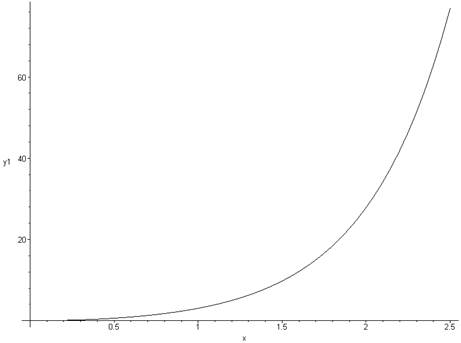
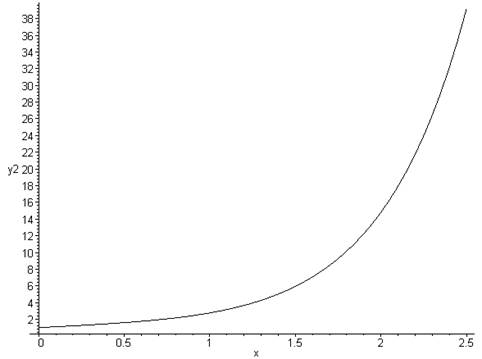
Решение системы двух ДУ с выводом графика

> restart;

> sys:=diff(y(x),x)=2*z(x)*sin(x)-y(x)-x, diff(z(x),x)=y(x);

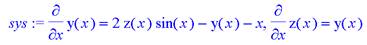
> f:={y(x),z(x)};

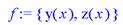
> P:=dsolve({sys,y(0)=0,z(0)=1},f,type=numeric,

output=listprocedure);

> Y:=subs(P,y(x)); Z:=subs(P,z(x));

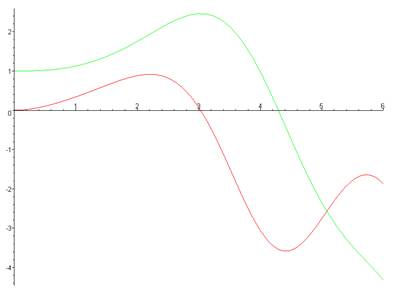
> plot({Y,Z},0..6);