Решение систем дифференциальных уравнений
Для решения таких систем использует функция dsolve(deqns,vars)или dsolve(deqns,vars,option) где
deqns – одно ДУ или система ДУ 1-го порядка с указанием начальных условий;
vars – переменная, относительно которых ищется решение;
option – необязательный параметр, указывающий на метод решения.
Параметр option задаёт один из методов решения:
exact – аналитическое решение (принято по умолчанию);
explicit – решение в явном виде;
laplace – решение через преобразования Лапласа.
Для решения задачи Коши в deqns надо включать начальные условия, а при решении краевых задач – краевые условия. Если Maple способна найти решение при числе начальных или краевых условий меньше порядка системы, то в решении будут появляться неопределённые константы вида _С1, _С2 и т.д. Они же могут быть при аналитическом решении системы, когда начальные условия не заданы. Если решение найдено в неявном виде, то в нём появится параметр _Т.
Производные при записи ДУ могут задаваться функцией diff или оператором D. Выражение deqns должно иметь структуру множества и содержать помимо самой системы уравнений их начальные условия.
Рассмотрим решение системы из двух дифференциальных уравнений различными методами – в явном виде, в виде разложения в ряд и с использованием преобразования Лапласа.
> sys:=diff(y(x),x)=2*z(x)-y(x)-x, diff(z(x),x)=y(x);
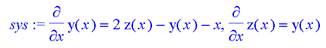
> fcns:={y(x),z(x)};
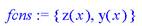
> dsolve({sys,y(0)=0,z(0)=1},fcns);
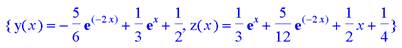
> order:=8;dsolve({sys,y(0)=0,z(0)=1},fcns,series);
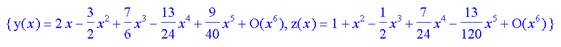
> dsolve({sys,y(0)=0,z(0)=1},fcns,laplace);
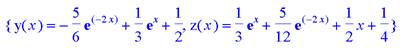
Дата добавления: 2020-10-01; просмотров: 492;











