Аналогично сумма всех диаграмм с показателем связности 3 имеет вид

и т.д. Таким образом, мы можем представить среднюю функцию Грина в виде диаграммного ряда

+

=

+

+

(30.13)

+

+

…

Соответствующая формула отличается от исходного ряда (30.6) только перегруппировкой членов.

Убедимся, что ряд (30.13) является решением уравнения

, (30.14)

которое носит название уравнения Дайсона. В аналитической форме (30.14) имеет вид

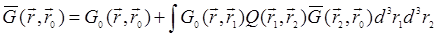(30.14а)

Чтобы показать, что (30.13) есть решение уравнения (30.14), найдем это решение, пользуясь последовательными итерациями в графической форме. Подставляя (30.14) в правую часть (30.14), получаем:

( ) =

=

Повторяя операцию, придем к ряду (30.13). Очевидно из изложенного, что те же самые выкладки можно было бы проделать в аналитической форме, исходя их уравнения (30.14а). Рекомендую вам проделать их самостоятельно, что, несомненно, подкрепит ваше доверие к графическим преобразованиям диаграмм.

Уравнение Дайсона, если считать в нем функцию Q известной, представляет собой линейное интегральное уравнение относительно 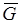, которое во многих случаях может быть решено. Особенно важным для нас является случай неограниченной рассеивающей биосреды, для которого из уравнения Дайсона с помощью диаграммной техники получается уравнение переноса излучения (УПИ). Однако рамки семестрового курса, увы, ограничивают возможности настолько подробного рассмотрения диаграммной техники, насколько эта мощная методика заслуживает. Поэтому, если мне удалось хоть в какой-то степени заинтересовать вас фейнмановскими диаграммами (по моему мнению, если бы Фейнман создал только их, он уже заслужил Нобелевскую премию, но жадный Нобелевский комитет присудил ее Фейнману по совокупности работ по квантовой теории поля), то отсылаю вас к литературе [1,2].

Литература к главе 30.

1. С.М. Рытов, Ю.А. Кравцов, В.И. Татарский. Введение в статистическую радиофизику. Ч.II. Случайные поля. – М.: Наука, 1978.

2. В.И. Татарский. Распространение волн в турбулентной атмосфере. – М.: Наука, 1967.