Расчеты на жесткость
Основы сопротивления материалов
Введение. Основные понятия и определения
Изделия техники: машины и механизмы, конструкции и сооружения должны удовлетворять требованиям надежности и экономичности при их изготовлении и эксплуатации. Часто выход из строя одной части конструкции или детали механизма приводит к разрушению всего изделия. Поэтому требованиям надежности и экономичности должны удовлетворять отдельные элементы машин, конструкций и сооружений, от чего зависит их работоспособность. Это основная цель «Сопротивления материалов».
Отдельную часть конструкции, сооружения или деталь машины условимся называть элементом конструкции (ЭК).
Сопротивление материалов (СМ) – наука об инженерных методах расчетов элементов конструкций (ЭК) на прочность, жесткость и устойчивость с целью обеспечения требуемой надежности и экономичности, минимальной материалоёмкости.
Под экономичностью конструкции подразумевается его минимальные материалоёмкость и затраты на изготовление и эксплуатацию.
Надежность конструкции – способность выполнять заданные функции, сохраняя свои нормативные эксплуатационные качества в течение требуемого срока работы.
Основная количественная характеристика надежности - это вероятность безотказной работы конструкции, определяемой требуемым ресурсом.
Прочность – способность конструкции или отдельных ее частей противостоять внешней нагрузке, не разрушаясь. Под внешней нагрузкой подразумевается совокупность внешних сил и моментов, действующих на конструкцию в целом и ее элементы.
Жесткость – способность конструкции или отдельных ее частей противостоять внешней нагрузке от изменения первоначальных форм и размеров.
Количественное выражение изменения формы и размеров ЭК и всей конструкции в целом называется деформацией.
Типы деформаций:
1) с геометрической точки зрения: линейные и угловые;
2) с физической точки зрения: упругие и пластичные (материалы: упругие, пластичные, упруго-пластичные);
3) по условиям нагружения: растяжение-сжатие, сдвиг (срез), кручение и изгиб.
Устойчивость – способность ЭК или конструкции в целом сохранять заданную форму упругого равновесия при внешней нагрузке.
2. Расчетная модель (схема)
При решении задач сопротивления материалов используются приемы моделирования. От правильности выбора критериев моделирования в конечном итоге зависят правильность и точность расчетов.
Элементы конструкций условно рассматриваются как модели (расчетные схемы).
Модель (расчетная схема) – совокупность представлений, зависимостей, условий, ограничений, описывающих процесс, явление.
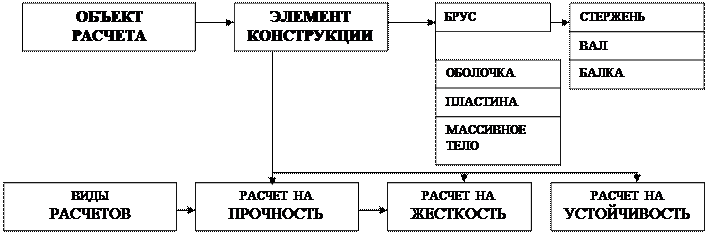
Рис. 1. Структурная схема задач сопротивления материалов
Модель (расчетная схема) получают из реального объекта и оставляют основные свойства, которые могут быть описаны математическими уравнениями. Погрешность при этом должна быть в пределах допустимой (до 5%).
Величина погрешности при создании и решении модели не должна противоречить требованиям ее надежности и должна гарантировать требуемые эксплуатационные показатели и ресурс, а также экономичность.
3.Составные части модели прочностной надежности
Совокупность свойств расчётной модели (схемы) называют моделью прочностной надёжности. Эти свойства даны в таблице 1.
|
|
|
|
|

|
|
|



|






3.1. Конструкционные материалы и их модели
В качестве конструкционных материалов в машиностроении используются в основном металлы и их сплавы, а также различные органические и неорганические материалы (полимеры, пластмассы, керамика, композитные материалы).
В сопротивлении материалов используются гипотезы о том, что материалы имеют сплошную однородную среду. Материал считается изотропным, т.е. свойства его по любым направлениям одинаковы. Считается, что материалы, абсолютно упругие и деформируемые, подчинятся закону Гука. Деформации малы в сравнении с первоначальными размерами ЭК, то есть должны выполняться принцип неизменности первоначальных размеров и принцип независимости действия сил. Это означает, что результат воздействия на реальный объект (ЭК) системы сил эквивалентен сумме результатов действия тех же сил, приложенных отдельно в произвольной последовательности (т.е. справедлив принцип суперпозиции и принцип Сен-Венана: в точках, достаточно удалённых от мест приложения нагрузок, внутренние силы весьма мало зависят от способа приложения нагрузок).
3.2. Модели формы
Геометрическая форма элементов конструкций часто бывает весьма сложной. Для определения напряженного и деформационного состояния применяют упрощенные схематизированные модели формы элементов конструкций с помощью стандартных типовых форм. Основными моделями формы являются брусья, пластины, оболочки, массивные тела.
Брус – геометрическое тело, у которого размеры сечения значительно меньше длины. Сечение, перпендикулярное оси бруса, называется поперечным сечением.
Линия, проходящая через центры тяжести поперечных сечений, называется осью бруса.
Брус, работающий на растяжение-сжатие, называют стержнем.
Брус, работающий на кручение, называют валом. В машинах и механизмах валы, в основном, работают при совместном действии изгиба и кручения. Брус, работающий на изгиб, называется балкой. Так как размеры сечения бруса (b и h) значительно меньше длины (l), в расчетных моделях брусья (валы, балки) изображают в виде сплошных линий, совпадающих с их осями. Брус – основной объект расчёта в сопротивлении материалов.
При деформировании используется гипотеза плоских сечений: сечения плоские до деформации остаются плоскими после деформации (гипотеза Бернулли).
Оболочками называются геометрические формы, ограниченные двумя близкими поверхностями.
Пластины ограничиваются двумя плоскими или слабоизогнутыми поверхностями (крыши зданий, палубы судов, люки и т.п.)
Массивное тело (массив) – модель элемента конструкции, в котором все размеры соизмеримы и являются величиной одного и того же порядка.
Реальные детали машин со сложной геометрией можно рассматривать как сочетание простых моделей формы.
Модели формы, их синтез имеют существенное значение для автоматизированного проектирования и конструирования (САПР).
3.3 Модели внешнего нагружения
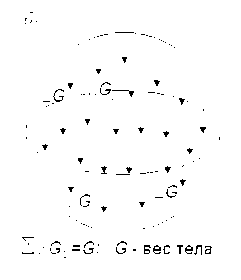
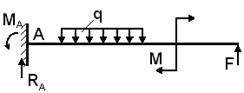
Как известно, сила – мера механического взаимодействия тел. Если конструкцию или ЭК рассматривать изолировано от взаимодействующих с ними тел, действие последних заменяется силами, которые называются внешними силами. Внешние силы деформируют тело. Внешние силы, действующие на элемент конструкции, подразделяют на три группы (рис.2):
1. Сосредоточенные силы (F) – силы, действующие на небольших участках поверхности детали или элемента конструкции (рис.2-а, в).
2. Распределенные силы(q1,2 )– силы, действующие на значительных участках поверхности (рис.2-а).
3. Объемные или массовые силы, – например, силы тяжести, инерции, электромагнитного притяжения (рис. 2-б).
Совокупность внешних сил, действующих на твёрдое тело, называют нагрузкой.
Возможно изменение сил во времени, определяемое условиями эксплуатации и параметрами рабочего процесса изделия: цикличность нагрузки, внезапные удары, имеющие вероятностный характер, вибрации. По характеру длительности действия принято различать нагрузки статические и динамические.
Статическая нагрузка – нагрузка, не изменяющаяся с течением времени (собственный вес конструкции) или изменяющаяся медленно, так что эффектом ускорения можно пренебречь.
Динамическая нагрузка – это нагрузка, учитывающая ускорения взаимодействующих тел. Динамическая нагрузка в отличие от статической меняет свое значение, положение или направление в короткие промежутки времени (движущие нагрузки, ударные, сейсмические и др.), вызывая большие ускорения и силы инерции, что приводит к определенному характеру деформирования и к колебаниям конструкций и сооружений. Динамические нагрузки делят на ударные, повторно-переменные и инерционные. Динамические нагрузки являются функцией времени.
Ударная нагрузка в момент ее приложения обладает определенной кинетической энергией.
Повторно-переменные нагрузки – нагрузки, которые во времени изменяются циклически (например, при вращении валов возникает совместное переменное действие изгиба и кручения).
3.4. Модели разрушения
Под разрушением в СМ понимается переход конструкции в такое состояние, при котором его дальнейшая эксплуатация становится невозможной. Внешние признаки разрушения проявляются в макроскопическом нарушении сплошности материала под действием чрезмерных внешних нагрузок. Разрушение проявляется также в появлении недопустимых остаточных деформаций и первичных трещин в ответственных конструкциях. При начале разрушения дальнейшая эксплуатация конструкции недопустима во избежание катастрофических последствий.
Модели разрушения – это совокупность условий (уравнений), которые связывают параметры работоспособности изделия или его отдельной части (элемента конструкции) в момент разрушения с параметрами, обеспечивающими прочность.
При этом подразумевается начало перехода от состояния прочности к началу разрушения. Эти условия называют условиями прочности.
 а) а)

| б)
|
в)
|
Рис.2. Виды нагрузок
а) нагрузки, действующие на твердое тело:
q1 – нагрузка, распределенная по линии (Н/м);
q2 – нагрузка, распределенная по площади (Н/м2);
F1, F2 – сосредоточенные силы (Н).
б) нагрузка, распределенная по объему тела Н/м3, G – сила веса;
в) нагрузки, действующие по длине балки:
активные силы: q – распределенная нагрузка,
М – сосредоточенный момент (Нм),
F – сосредоточенная сила (Н),
реактивные силы: RА – опорная реакция (Н),
МА – реактивный момент (Нм).
Процесс разрушения сопровождается упругой и пластической деформациями. Различают следующие модели разрушений в зависимости от условий нагружения и вида деформирования.
Статическое разрушение - пластическая деформация развивается при постоянной нагрузке. Характер разрушения – пластический (со значительной остаточной деформацией) или хрупкий (с малой остаточной деформацией).
Длительное статическое разрушение – при значительных температурах развивается ползучесть, пластические деформации увеличиваются с течением времени при постоянной нагрузке, что приводит к разрушению.
Усталостное разрушение - наступает после многократных циклически изменяющихся, нагрузках. Разрушение происходит при отсутствии видимых пластических деформаций. При этом разрушение происходит в том месте детали, где имеется концентратор напряжений, появляется трещина и распространяется по объему материала.
Малоцикловое разрушение – разрушение, которое носит смешанный пластический и хрупкий характер.
Вопросы к 1-3
1. Какие задачи решает сопротивление материалов?
2. Что такое элемент конструкции?
3. Понятия о надежности и экономичности.
4. Что такое прочность, жесткость и устойчивость?
5. Что называется расчетной моделью?
6. Понятия о модели прочностной надежности.
7. Понятия о брусе, оболочке, пластине и массивном теле.
8. Что такое стержень, вал и балка?
9. Как условно изображается и обозначается внешняя нагрузка?
10. Классификация внешней нагрузки.
11. Модели формы материала.
12. Как классифицируются виды разрушения?
Тесты к 1-3
1. Сопротивление материалов – это наука:
а) о действии нагрузок на конструкции;
б) об инженерных методах расчета на прочность, жесткость и устойчивость элементов конструкции;
в) об упругости материальных тел.
2. Прочность конструкции
а) способность противостоять коррозии;
б) способность элемента конструкции растягиваться или сжиматься;
в) способность конструкции противостоять внешней нагрузке, не разрушаясь.
3. Жесткость конструкции
а) свойство подвергаться технологической обработке;
б) способность конструкции сохранять свои формы и размеры при действии внешней нагрузки;
в) способность противостоять вибрациям.
4. Устойчивость конструкции
а) способность сохранять заданную форму упругого равновесия;
б) способность противостоять опрокидыванию;
в) способность возвращаться в исходное положение при нагружении.
5. Расчетная модель
а) изготовление макета конструкции;
б) изготовление чертежей и эскизов конструкции;
в) совокупность аналогий реального объекта при отбрасывании от него второстепенных подробностей, что упрощает расчет.
Литература
[2, стр. 4-21]; [6, стр. 5-20], [5, стр. 5-15].
4. Внутренние силовые факторы (ВСФ)
4.1. Метод сечений
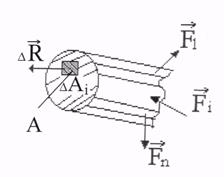
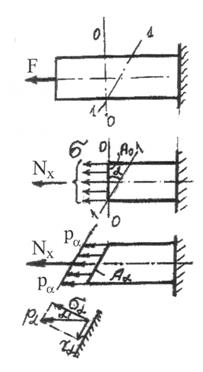
При деформировании упругих тел под действием внешней нагрузки возникают силы противодействия деформированию - внутренние силы. Пока не произойдет разрушение тела, внешние силы уравновешиваются внутренними. Природа внутренних сил – атомарное и молекулярное взаимодействие частиц тела. Внутренние силы или внутренние силовые факторы (ВСФ) определяются методом сечений.
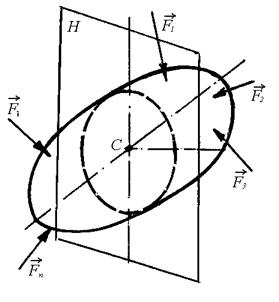
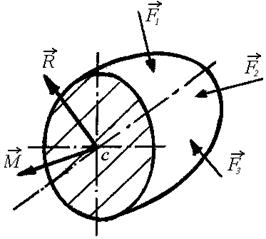
Сущность метода сечений: упругое твердое тело, несущее внешнюю нагрузку, уравновешиваемую телом, мысленно рассекается плоскостью. Если тело – брус и секущая плоскость проводится перпендикулярно его оси, получают поперечное сечение.
Затем рассматривается условие равновесия каждой отсеченной части, то есть определяются сила и момент, которые, будучи приложенными в центре тяжести сечения, уравновесят внешнюю нагрузку, действующую на  рассматриваемую отсеченную часть. Эта сила и момент, приложенные в центре тяжести сечения, являются соответственно главным вектором
рассматриваемую отсеченную часть. Эта сила и момент, приложенные в центре тяжести сечения, являются соответственно главным вектором  и
и  главным моментом внутренних сил -
главным моментом внутренних сил -  (рис. 3-б).
(рис. 3-б).
а)
| б)
|
в)
| H – секущая плоскость;
С – центр тяжести сечения;
Силы Fί действуют на одну сторону сечения
ί = 1,2,... ,n
→
R - главный вектор внутренних сил;
→ n
R = ∑ Fί
ί=1
→
M- главный момент внутренних сил.
→ → →
M = ∑ Mί (Fί)
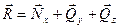
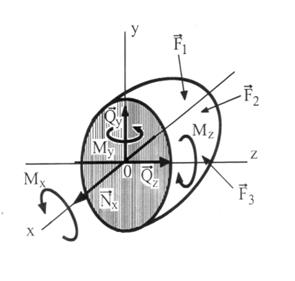
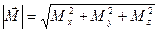 Nx, Qy, Qz, Mx, My, Mz – внутренние силовые факторы.
Nx, Qy, Qz, Mx, My, Mz – внутренние силовые факторы.
|
Рис.3 Метод сечений.
На рис.3 (а, б, в) показана последовательность определения ВСФ по методу сечений.
Через центр тяжести сечения проводят три взаимно перпендикулярные оси. При этом ось х перпендикулярна сечению, а оси y и z проходят по поверхности сечения, совпадая с его главными осями. Определяют составляющие главных вектора  и момента
и момента 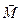 относительно осей x, y, z. (рис.3-в)
относительно осей x, y, z. (рис.3-в)
Nx - сила, перпендикулярная сечению, Qy и Qz – силы, действующие по поверхности сечения, Mx, My, Mz – моменты относительно соответствующих осей (рис. 3-в). Таким образом, в общем случае в сечении тела действуют шесть внутренних силовых факторов, величины и направление которых можно определить с помощью шести уравнений статики для пространственной системы сил:
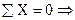 (определяется) Nx;
(определяется) Nx;  mx = 0
mx = 0 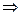 (определяется) Mx;
(определяется) Mx; 
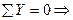 (определяется) Qy;
(определяется) Qy;  my = 0
my = 0 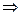 (определяется) My;
(определяется) My;
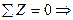 (определяется) Qz;
(определяется) Qz;  mz = 0
mz = 0 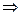 (определяется) Mz;
(определяется) Mz;


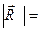
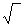 Nx2 + Qx2 + Qz2
Nx2 + Qx2 + Qz2 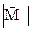 =
= 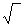 Мx2 + Мy2 + Мz2
Мx2 + Мy2 + Мz2
Вопросы к 4
1. В чём сущность метода сечений?
2. Чему равен главный вектор и главный момент внутренних сил?
3. Как определяют внутренние силовые факторы?
4. Типы деформаций.
5. В чём заключается количественная оценка деформаций?
Тесты к 4
4.1. Метод сечений
а) метод определения центра тяжести сечения;
б) метод выявления внутренних сил в сечении нагруженного тела;
в) метод определения сил при растяжении – сжатии.
4.2. Какие внутренние силовые факторы действуют в сечении нагруженного тела?
а) силы растяжения, сдвига, моментов изгиба и кручения;
б) силы молекулярного притяжения;
в) электромагнитные гравитационные силы.
4.3. Главный вектор внутренних сил равен сумме сил внешних, действующих по одну сторону сечения?
а) да;
б) нет;
в) равен главному вектору внешних сил.
4.4. Главный вектор внутренних сил определяется методом сечений?
а) нет;
б) да;
в) определяется аналитически.
4.5. Главный момент внутренних сил определяет моменты изгиба?
а) нет;
б) да;
в) внешние силы.
Литература
[2, стр. 4-88]; [5, стр. 11 -16, 22-78].
5. Напряжение
Напряжение – мера интенсивности внутренних сил, распределенных в сечении деформируемого тела по определенному закону.
Оптимальная величина напряжений – основной критерий прочности материала. Если напряжения во всех сечениях ЭК равны максимально допустимым, то конструкция является равнопрочной и минимально материалоемкой.
Единица измерения напряжения – мегапаскаль (МПа)
1 МПа = 1 Н/мм2
 - внутренняя сила, действующая на элементарной площадке сечения
- внутренняя сила, действующая на элементарной площадке сечения  , (Н)
, (Н)
 -площадь элементарной площадки, (мм2) (рис.4)
-площадь элементарной площадки, (мм2) (рис.4)
| А – площадь сечения, (мм2); А = 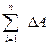 i, i =1,2, …, n
рср - полное среднее напряжение на элементарной площадке i, i =1,2, …, n
рср - полное среднее напряжение на элементарной площадке  , (Н/мм2, МПа)
р – полное напряжение на элементарной площадке , (Н/мм2, МПа)
р – полное напряжение на элементарной площадке 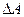 (Н/мм2, МПа) (Н/мм2, МПа)
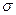 - нормальное напряжение, (МПа) - нормальное напряжение, (МПа)
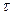 - касательное напряжение, (МПа) - касательное напряжение, (МПа)  n-n – внешняя нормаль к площадке А (рис.5)
n-n – внешняя нормаль к площадке А (рис.5)
| ||
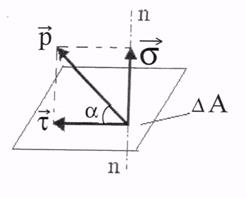 Рис.5
Рис.5
|
 ср. = ср. = 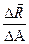 ; ; 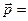 lim lim  ; ; 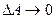 ; ;
 ; ; 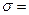 р sin р sin 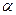 ; ;  р cos р cos 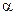
| ||


Таблица 2
| Типы деформации | Схема сил и напряжений | Напряжения, выраженные через внутренние силовые факторы |
Осевое растяжение-сжатие:
Направление силы F совпадает с осью бруса (стержня). В сечении бруса действует обобщенная внутренняя осевая сила Nx= 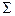 Fi. Внутренняя сила Nx распределяется равномерно в поперечном сечении 0-0 в виде нормальных напряжений Fi. Внутренняя сила Nx распределяется равномерно в поперечном сечении 0-0 в виде нормальных напряжений 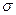 . В наклонном сечении – в виде нормальных . В наклонном сечении – в виде нормальных 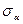 и касательных напряжений и касательных напряжений 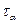 . Закон Гука при растяжении-сжатии: ∆ℓ−ℓ1−ℓ0 абсолютное удлинение стержня (мм)
ε =∆ℓ/ℓ - относительное удлинение стержня, А - площадь сечения (мм)
∆ℓ=F· ℓ0 / E ·А . Закон Гука при растяжении-сжатии: ∆ℓ−ℓ1−ℓ0 абсолютное удлинение стержня (мм)
ε =∆ℓ/ℓ - относительное удлинение стержня, А - площадь сечения (мм)
∆ℓ=F· ℓ0 / E ·А
| 
| Nx = 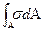  const const
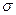 = Nx / A0 = F / A0
Nx = = Nx / A0 = F / A0
Nx = 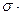 A0 ;
Nx = A0 ;
Nx = 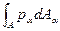
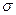 >0 – при растяжении >0 – при растяжении
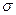 <0 – при сжатии
рa = <0 – при сжатии
рa = 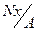 = = 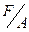 sa
sa  нормальные и
касательные
ta напряжения наклоном
сечении 1-1
sa = рa cos a; ta = pa sina
sa = scos2 ta = 1/2ssin2a
sa max = s (в сечении 0-0)
ta max = s / 2 (при a = 450) нормальные и
касательные
ta напряжения наклоном
сечении 1-1
sa = рa cos a; ta = pa sina
sa = scos2 ta = 1/2ssin2a
sa max = s (в сечении 0-0)
ta max = s / 2 (при a = 450)
|
 Сдвиг (срез): в поперечном сечении бруса действует сила Q, распределенная равномерно по поверхности сечения в виде касательных напряжений Сдвиг (срез): в поперечном сечении бруса действует сила Q, распределенная равномерно по поверхности сечения в виде касательных напряжений
| 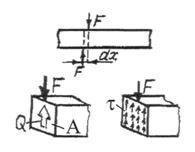
| Q = F = òAt × dA Q = t × A t = const t = Q/A |
Кручение: в поперечном сечении вала действует крутящий момент m = Мx = Мк распределенный по поверхности сечений в виде касательных напряжений 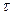 по линейному закону. По краям сечения по линейному закону. По краям сечения  max, в центре max, в центре  .
Мк - положительный, т.е. Мк>0, если направление его действия – против часовой стрелки, а наоборот Мк<0 .
Мк - положительный, т.е. Мк>0, если направление его действия – против часовой стрелки, а наоборот Мк<0
| 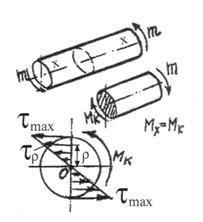
| Mk = òAtpdAp; tp = Mkp/Jp Jr = òAr2 dA; Jr = pD4 / 32 – полярный момент инерции (мм4); Wr = Jr / rmax = pD3 / 16 – полярный момент сопротивления (мм3) tmax = Mk tmax / Jmax = Mk / Wr tmax = Mk / Wr |
Изгиб (чистый): изгибающий момент Мu, действующий в плоскости симметрии, распределяется по поверхности сечения в виде нормальных напряжений 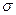 по линейному закону. по линейному закону. 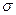 max – в крайних точках сечения по оси Y, max – в крайних точках сечения по оси Y,
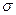 = 0 – в центре сечения. = 0 – в центре сечения.
| 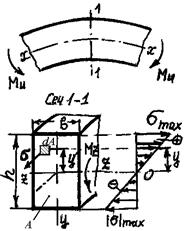
| Mu = òAs × dA × y s = Mu × y / Jz smax = Mu × y max / Jz Jx = òAy2dA – осевой момент инерции smax = Mu / Wz Wz = Jz / ymax – осевой момент сопротивления Jz = bh3 /12; Wz = bh2 / 6(1) Jy = hb3 /12; Wz = hb2 / 6(2) Jz(y) = pD4/64;Wz(y) = pD3/3 (для круга) |
Если в сечении действуют несколько ВСФ, то имеет место сложное сопротивление
Вопросы к 5
1. Что такое напряжение? Виды напряжений.
2. В каких единицах измеряются напряжения?
3. Чем отличаются нормальные напряжения от касательных?
4. Что оценивается величиной напряжений?
5. Что такое равнопрочная конструкция?
Тесты к 5
5.1. Напряжения нормальные возникают:
а) при растяжении – сжатии и изгибе;
б) при сдвиге – срезе;
в) при статическом нагружении.
5.2. Типы напряжений:
а) при ударе;
б) при ускоренном движении;
в) нормальные (σ), касательные (τ).
5.3. В наклонном сечении нагруженного стержня осевыми нагрузками возникают:
а) силы сдвига;
б) нормальные (σ) и касательные напряжения (τ);
в) продольные деформации.
5.4. При кручении в нормальном сечении вала возникают:
а) касательные напряжения;
б) нормальные напряжения
в) момент сопротивления ( Wp).
5.5 При чистом изгибе в поперечном сечении балки возникают:
а) поперечные силы (Q);
б) касательные напряжения (τ);
в) нормальные напряжения (σ).
Литература
[2, стр. 135-165]; [5, стр. 121-132].
6. Механические характеристики материалов
При проектировании, при расчетах элементов конструкций на прочность, жесткость и устойчивость и выборе соответствующих материалов необходимо знать их механические характеристики. К механическим характеристикам материалов относятся:
1. Упругость – способность материала восстанавливать свои первоначальные формы и размеры после снятия внешних нагрузок. Упругие свойства материалов характеризуют величины пределов пропорциональности ( 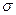 пц) и упругости (
пц) и упругости ( 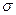 у).
у).
2. Пластичность – способность материала приобретать пластические неисчезающие деформации после снятия внешней нагрузки. Пластичность материала характеризуется пределом текучести ( 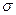 т) и коэффициентами остаточного удлинения (
т) и коэффициентами остаточного удлинения (  ) и сужения шейки (
) и сужения шейки ( 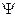 ) испытуемого образца.
) испытуемого образца.
3. Прочность при статическом нагружении. Оценивается по пределам прочности (временное сопротивление) 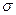 в и текучести материалов
в и текучести материалов 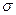 т. По
т. По 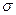 в оценивается прочность хрупких материалов, по
в оценивается прочность хрупких материалов, по 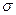 т - прочность пластичных материалов.
т - прочность пластичных материалов.
4. Прочность при ударной нагрузке – способность материала противостоять ударной нагрузке, оценивается по ударной вязкости материала “a”.
5. Выносливость материала или усталостная прочность – способность материала противостоять воздействию циклически изменяющихся напряжений. Выносливость материала оценивается по величине предела выносливости, как правило, при симметричном цикле нагружения ( 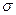 -1) как наиболее опасном.
-1) как наиболее опасном.
6. Твердость материала связана соотношением с пределом прочности материала и определяется на ряде приборов посредством вдавливания в поверхность материала шарика, конуса, алмазной пирамиды (методы определения твердости по приборам Бринеля, Роквелла, Виккерса и др.).
Механические характеристики определяются экспериментальным путем в лабораторных условиях посредством испытания образцов, стандартной формы.
По результатам испытаний строятся диаграммы, например растяжения и сжатия. Механические характеристики материала и их обозначения даны в табл. 3.
Таблица 3.
Механические характеристики материалов

При сжатии характеристики механической прочности пластичных материалов вплоть до предела текучести совпадают с их значениями при растяжении:
sуп(сж) » sуп (раст), sпц(сж) » sпц(раст), sт(сж) » sт(раст)
Предел прочности (временное сопротивление) при сжатии зафиксировать практически невозможно. Образцы сплющиваются, принимают “лепесткообразную форму”. Для хрупких материалов предел прочности при сжатии значительно больше предела прочности при растяжении (sв сж>sв раст, 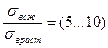 )
)
Различают два основных вида конструкционных материалов: хрупкие и пластичные. Хрупкие материалы разрушаются при незначительной остаточной деформации (высокоуглеродистые и легированные стали, стекло, бетон и т.д.) без образовании шейки на поверхности образцов.
| 
|
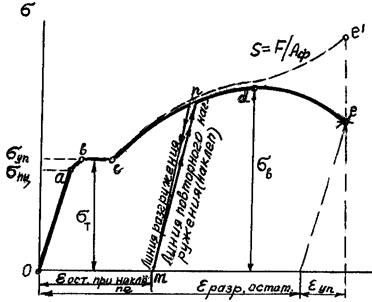
Рис.6 Диаграмма растяжения пластичного
материала (сталь 3)
I. «Da», ав - зона упругого деформирования ( 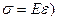 II. bc – площадка текучести
III. cd – зона упрочнения
IV. de – зона разрушения
n-m – линия разгружения (
II. bc – площадка текучести
III. cd – зона упрочнения
IV. de – зона разрушения
n-m – линия разгружения ( 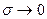 )
m-n - линия повторного нагружения, упругие свойства проявляются (повышаются) до точки n – это наклёп
c-e – линия истинных напряжений
Аф – фактическая площадь поперечного сечения при растяжении. )
m-n - линия повторного нагружения, упругие свойства проявляются (повышаются) до точки n – это наклёп
c-e – линия истинных напряжений
Аф – фактическая площадь поперечного сечения при растяжении.
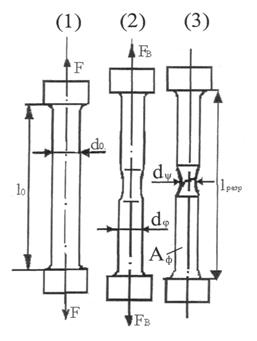
| Рис.7 Эскизы образцов:
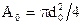 ; ; 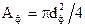 ; ; 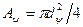 (1) – в начале испытаний
(2) – начало разрушения
(3) – после разрушения
(1) – в начале испытаний
(2) – начало разрушения
(3) – после разрушения
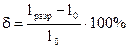 - коэффициент остаточного удлинения. - коэффициент остаточного удлинения.
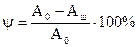 - коэффициент сужения шейки - коэффициент сужения шейки
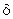 и и 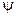 - характеризуют пластичность материала - характеризуют пластичность материала
|
Пластичные материалы (малоуглеродистая сталь, золото, платина, свинец и т.д.) разрушаются при значительных остаточных деформациях. Образцы из малоуглеродистой стали разрушаются с образованием шейки (рис.7). Механические характеристики используются для определения допускаемых напряжений и деформаций.
На рис.6 дана диаграмма растяжения образца из малоуглеродистой стали и эскизы испытуемых образцов до и после испытаний. Диаграмма растяжения дает возможность наиболее полного получения механических характеристик пластичного материала при статическом нагружении.
6.1.Коэффициент Пуассона
Коэффициент Пуассона (n) совместно с модулем упругости (Е и G) является константой, характеризующей упругие свойства материала и связанные между собой зависимостью G= Е / 2(1+n)
Коэффициент Пуассона (n) определяется экспериментально или дается в справочниках для рассматриваемого материала.
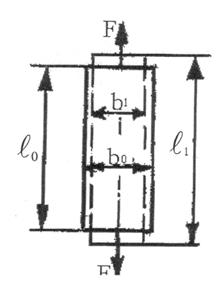 Рис.8 Определение коэффициента Пуассона
Рис.8 Определение коэффициента Пуассона
| Коэффициент поперечной деформации (рис.8)
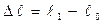 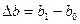 (определяются тензометрами) (определяются тензометрами)
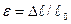 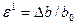
 - коэффициент Пуассона
n - характеризует упругие свойства материалов
n = 0…0,5 (см. табл.)
n = 0,25…0,35 (для стали)
Значения ²n² одинаковы при сжатии и растяжении - коэффициент Пуассона
n - характеризует упругие свойства материалов
n = 0…0,5 (см. табл.)
n = 0,25…0,35 (для стали)
Значения ²n² одинаковы при сжатии и растяжении
|
На рис.9 дана схема испытания образцов на ударную вязкость. Ударная вязкость характеризует прочность материалов при динамических нагрузках.
На рис.10 даны схемы определения твердости материалов. Твердость материала связана количественно с пределом прочности материала и служит в качестве экспресс-метода экспериментальной оценки прочности материалов.

|

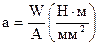 ; ; 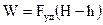
|
Рис.9 Схема испытаний образцов на ударную вязкость
а) б)
|
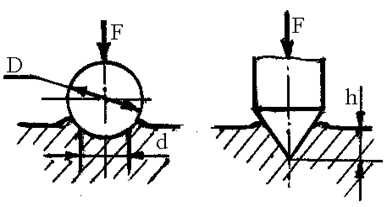
Рис.10 а) Определение твердости материала по Бри Нелю НВ » 0,35sв
б) Определение твердости по Роквеллу
Вопросы к 6
1. Для чего необходимо знать механические характеристики материала?
2. Перечислите характеристики механической прочности.
3. В чем особенность диаграммы растяжения пластичных материалов?
4. Назовите характеристики пластичности материала.
5. Сравните механические характеристики при растяжении и сжатии?
6. Что такое испытания на ударную вязкость?
7. Для чего определяют твердость материалов?
8. Какие материалы называются пластичными, а также хрупкими?
Тесты к 6
Механические характеристики материалов
6.1. Упругость
а) способность материала изгибаться;
б) способность материала восстанавливать свою форму и размеры после снятия внешней нагрузки;
в) характеристика пружин и рессор.
6.2. Пластичность
а) способность материала приобретать остаточные пластические неисчезающие деформации;
б) свойство пластических масс при нагревании;
в) способность материала при ковке принимать необходимые формы.
6.3. Пластичность характеризуется:
а) пределом пропорциональности;
б) пределом текучести;
в) коэффициентом остаточного удлинения (d) и остаточного сужуния шейки (ψ) испытуемого образца.
6.4. Твердость материала:
а) способность материала к механической обработке;
б) способность материала противодействовать механическому проникновению в него инородных (посторонних) тел;
в) свойства, присущие твердым сплавам и алмазу.
6.5. Характеристики механической прочности:
а) модули упругости Е и G;
б) коэффициент Пуассона;
в) пределы пропорциональности sпц, упругости sуп, предел текучести sт, предел прочности sв
Литература
[2, стр. 33-56]; [6, стр. 26-56].
7. Геометрические характеристики плоских сечений (ГХПС)
ГХПС – необходимы для решения задач СМ
Дата добавления: 2020-08-31; просмотров: 923;











