Критические напряжения при сжатии стержня
sкр=Fкр/А=(p2 EJmin)/(m 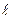 )2 A=(p2 E)/[ (m
)2 A=(p2 E)/[ (m 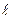 )2/Jmin/A], sкр = p2 E/l2
)2/Jmin/A], sкр = p2 E/l2
l- гибкость стержня, l = m 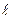 /imin
/imin
A– площадь сечения (мм2)
imin – радиус инерции сечения (мм), где
imin = 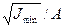 i2min = Jmin/A
i2min = Jmin/A
11.3. Определение критических напряжений при различных величинах гибкости стержня λ.
Таблица 7
| Гибкость стержня | Критические напряжения | |
| Стержни большой гибкости | l³100 | Формула Эйлера: sk=p2E/l2 |
| Стержни средней гибкости | 100>l³40 | Зависимость Ясинского: sk=а-bl а и b табличные величины |
| Стержни малой гибкости | l>40 | sк = sт |
Абр – площадь сечения “брутто” (по внешнему и внутреннему контурам)
Вопросы к 11
1. Чем опасна потеря устойчивости?
2. Причины потери устойчивости.
3. Объясните формулу Эйлера и предел ее применимости.
4. Когда применяется зависимость Ясинского?
5. Критические напряжения.
6. Порядок расчёта сжатых стержней на устойчивость.
7. Рациональное расположение сечений для предотвращения потери устойчивости.
Тесты к 11
11.1. Критические силы
а) силы сжатия, при которых наступает предел текучести;
б) силы, при которых сжатый стержень теряет устойчивость, упругое равновесие;
в) силы, при которых стержень разрушается.
11.2. Потеря устойчивости происходит в результате продольного изгиба относительно главной оси сечения, относительно которой осевой момент инерции.
а) Jmin;
б) Jmax;
в) момент сопротивления максимальный.
11.3. Критические напряжения Эйлера должны быть:
а) меньше sв;
б) меньше sт;
в) при значениях l³100.
11.4. Зависимость Ясинского применяется, если:
а) sкр = sт;
б) 100≥ l ³40;
в) при imin= 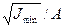
.
11.5. Условие устойчивости сжатого стержня:
а) sкр =Fкр/А =j [s]
б) sкр > sт;
в) [sу] = j[s]
Литература
[12, стр.483-506]; [5, стр.413-453].
12. Элементы теории напряженного состояния
12.1 Сложное напряженное состояние.
Если в нагруженном твёрдом теле выделить элементарный объём со сторонами dx, dy, dz , то на гранях этого объема, в общем случае, будут действовать напряжения: три нормальных, параллельных осям x, y, z и перпендикулярные граням (площадкам) “элементарного кубика” (sx, sy, sz), и на каждой грани - по паре взаимно перпендикулярных, напряжений параллельных рёбрам. Если менять ориентацию элементарного кубика, величина напряжений будет меняться. Существует единственное положение элементарного объёма, когда по его граням касательные напряжения равны нулю. Эти грани кубика называются – главными площадками, а перпендикулярные им напряжения – главными. Наибольшее из них обозначается s1, а наименьшее s3. Общее соотношение главных напряжений: s1 > s2 > s3 (с учётом знаков).
Существует три вида напряженных состояний:
1. Линейное, если действует только нормальное напряжение s1, а s2 = s3 = 0.
2. Плоское, когда действуют s1 и s2, а s3 = 0.
3. Объёмное, когда действуют s1 > s2 > s3 с учётом знака.
Величины главных напряжений и положение главных площадок оказывают решающее значение на прочность материала и на расчёты по принятым теориям прочности. В силу ограниченности объёма излагаемого материала, по данному пособию, студенту следует изучить данную тему по учебникам [2, стр. 91-107], [5, стр. 252-275].
12.2 Теории (гипотезы) прочности.
В настоящее время строго достоверная теория прочности ещё не разработана. Существующие теории (вернее гипотезы) не дают полного обоснования критерия разрушения. Предполагается, что принятый критерий прочности является ответственным за появление опасного (предельного) состояния, при данном виде нагружения. Одной из распространённых теорий прочности является теория касательных напряжений, называемая третьей теорией прочности. Согласно этой теории причиной разрушения являются максимальные касательные напряжения, когда они достигают опасной величины, при которой возникает текучесть материала при растяжении (или сжатии).
τmax ≤ [ τ]
или s1 - s3 ≤ [s]
Другой широко применяемой теорией прочности является энергетическая теория (4-ая теория) прочности, суть которой заключается в том, что опасное (предельное), состояние материала наступает тогда, когда удельная потенциальная энергия формоизменения достигает такой величины, при которой наступает текучесть или разрушение при растяжении (сжатии).
Подробно этот материал следует изучить по учебникам [2, стр. 340-355], [5, стр. 292-310].
Вопросы к 12
1. Понятие о сложном напряженном состоянии.
2. Какие площадки называются главными?
3. Какие напряжения называются главными?
4. Виды напряженного состояния.
5. Соотношение между главными напряжениями.
6. Понятие о теориях (гипотезах) прочности.
7. Какие теории (гипотезы) прочности применяются наиболее часто?
Тесты к 12
12.1. Главные напряжения:
а) нормальные и касательные напряжения;
б) нормальные напряжения, действующие на главных площадках;
в) касательные напряжения на главных площадках.
12.2. Соотношение между главными напряжениями.
а) s1 > s2 > s3;
б) s1 > s2 < s3;
в) s1 = s2 > s3.
12.3. Главное напряжение s1 - наибольшее?
а) да;
б) нет;
в) наибольшее s3.
12.4. Теории (гипотезы) полностью объясняют прочность материала?
а) да;
б) при нормальных температурах;
в) с некоторой погрешностью.
12.5. Какие теории (гипотезы) прочности наиболее достоверны?
а) 3я и 4я;
б) 1я и 2я;
в) smax ≤ [s] .
13. Сложное сопротивление
При сложном сопротивлении в поперечном сечении бруса могут возникать несколько внутренних силовых факторов (ВСФ). В общем случае шесть: Nx, Qy, Qz, Mx, My, Mz , которые в частных случаях являются причиной возникновения простейших типов деформации. Это – растяжение (сжатие), сдвиг (срез), кручение, изгиб.
Сочетание нескольких простейших типов деформаций, действующих одновременно, называется сложным сопротивлением.
Примеры сложного сопротивления: изгиб с кручением, изгиб с растяжением - сжатием, кручение с растяжением – сжатием, косой изгиб и т.д.
Расчет на прочность при сложном сопротивлении ведется путем определения приведенных напряжений, если в сечении действуют s и τ, по той или иной теории прочности и сравниваются [s] (см. рис.5-пр, стр58)
sпр ≤ [s]
Подробно вопросы расчетов на прочность и жесткость при сложном сопротивлении даны в учебниках [2, стр. 340-354], [6, стр. 195-214].
Дата добавления: 2020-08-31; просмотров: 551;











