Данные об объемах выпуска, затратах и прибыли
| объемы и затраты | цены и прибыли | ||||||||
| Y | C | AC | MC | ||||||
| -250 | -150 | -50 | |||||||
| 40,5 | -40 | +120 | |||||||
| 40,1 | -10 | ||||||||
| 40,3 | -40 | ||||||||
| 41,7 | -250 | ||||||||
| 42,9 | -490 | -150 | |||||||
| -1000 | -600 | -200 | |||||||
| 46,5 | -1440 | -1000 | -560 |
В случае же несовершенной конкуренции производитель может оказывать непосредственное влияние на цену. В особенности это относится к монопольному производителю товара, который формирует цену из соображения разумной рентабельности.
Рассмотрим фирму с линейной функцией издержек, которая определяет цену таким образом, чтобы прибыль составляла определенный процент (долю 0 < g < 1) от валового дохода, т.е.:
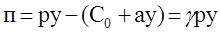 .
.
Отсюда имеем:
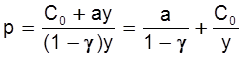 .
.
Валовый доход:
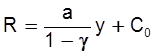
и производство оказывается безубыточным, начиная с самых малых объемов производства ( 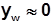 ). Легко видеть, что цена зависит от объема, т.е.p = p(y) и при увеличении объема производства (у) цена товара уменьшается, т.е.
). Легко видеть, что цена зависит от объема, т.е.p = p(y) и при увеличении объема производства (у) цена товара уменьшается, т.е. 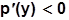 . Это положение имеет место для монополиста и в общем случае.
. Это положение имеет место для монополиста и в общем случае.
Требование максимизации прибыли для монополиста имеет вид:
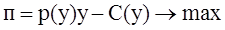
Предполагая по-прежнему, что 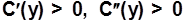 , имеем уравнение для нахождения оптимального выпуска (
, имеем уравнение для нахождения оптимального выпуска ( 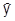 )
)
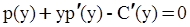
Полезно заметить, что оптимальный выпуск монополиста ( 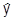 ), как правило, не превосходит оптимального выпуска конкурентного производителя
), как правило, не превосходит оптимального выпуска конкурентного производителя 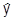 в формуле (*).
в формуле (*).
Более реалистичная (но также простая) модель фирмы используется для того, чтобы учесть ресурсные ограничения , которые играют очень большую роль в хозяйственной деятельности производителей. В модели выделяется один наиболее дефицитный ресурс (рабочая сила, основные фонды, редкий материал, энергия и т.п.) и предполагается, что фирма может его использовать не более, чем в количестве Q. Фирма может производить n различных продуктов. Пусть y1,..., yj,..., ynискомые объемы производства этих продуктов; p1,..., pj,..., pn –их цены. Пусть также q – цена единицы дефицитного ресурса. Тогда валовый доход фирмы равен

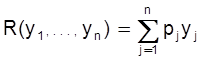 ,
,
а прибыль составит
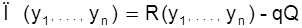 .
.
Легко видеть, что при фиксированных qиQ, задача о максимизации прибыли преобразуется в задачу максимизации валового дохода.
Предположим далее, что функция издержек ресурса для каждого продукта Cj(yj), обладает теми же свойствами, которые были высказаны выше для функции С(у). Таким образом, 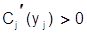 и
и 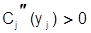 .
.
В окончательном виде модель оптимального поведения фирмы с одним ограниченным ресурсом следующая:
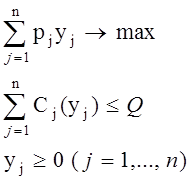
Нетрудно видеть, что в достаточно общем случае решением этой оптимизационной задачи находится путем исследования системы уравнений:
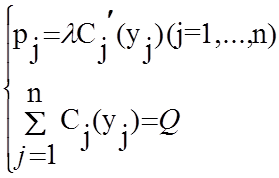 (**)
(**)
где l – множитель Лагранжа.
Заметим, что соотношение 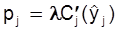 является по существу аналогом отмеченного выше совпадения в оптимальной точке маргинального дохода и маргинальных издержек. В случае квадратичных функций издержек
является по существу аналогом отмеченного выше совпадения в оптимальной точке маргинального дохода и маргинальных издержек. В случае квадратичных функций издержек 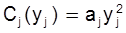 из системы (**) имеем:
из системы (**) имеем:
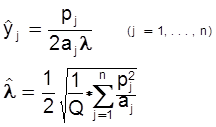 (***)
(***)
Заметим, что оптимальный выбор фирмы зависит от всей совокупности цен на продукты (p1,...,pn); причем этот выбор является однородной функцией системы цен, т.е. при одновременном изменении цен в одинаковое количество раз оптимальные выпуски 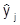 не изменяются. Нетрудно видеть также, что из (***) следует, что при увеличении цены на продукт j (при неизменных ценах на другие продукты) его выпуск следует увеличить с целью получения максимальной прибыли, т.е.:
не изменяются. Нетрудно видеть также, что из (***) следует, что при увеличении цены на продукт j (при неизменных ценах на другие продукты) его выпуск следует увеличить с целью получения максимальной прибыли, т.е.:
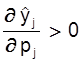 ,
,
а производство остальных товаров уменьшится, т.е.
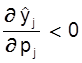 .
.
Эти соотношения в совокупности показывают, что в данной модели все продукты являются конкурирующими. Из формулы (***) вытекает также очевидное соотношение:
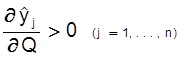 ,
,
т.е. при увеличении объема ресурса (капиталовложений, рабочей силы и т.п.) оптимальные выпуски увеличиваются.
В заключение параграфа приведем ряд простых примеров, которые помогут лучше понять правило оптимального выбора фирмы по принципу максимума прибыли:
1) пусть n = 2; p1 = p2 = 1; a1 = a2 = 1; Q = 0.5; q = 0.5.
Тогда из (***) имеем:
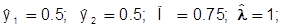
2) пусть теперь все условия остались прежними, но удвоилась цена на первый продукт: p1 = 2.
Тогда оптимальный по прибыли план фирмы: 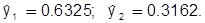
Ожидаемая максимальная прибыль заметно возрастает: 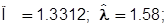
3) заметим, что в предыдущем примере 2, фирма должна изменить объемы производств, увеличив производство первого и уменьшив производство второго продукта. Предположим, однако, что фирма не гонится за максимальной прибылью и не станет менять налаженное производство, т.е. выберет программу y1=0.5; y2 = 0.5.
Оказывается, что в этом случае прибыль составит П = 1.25. Это означает, что при повышении цен на рынке фирма может получить значительное увеличение прибыли без изменения плана выпуска.
Дата добавления: 2016-05-30; просмотров: 1580;











