Моделирование издержек и прибыли предприятия (фирмы)

В основе построения моделей поведения производителя (отдельного предприятия или фирмы; объединения или отрасли) лежит представление о том, что производитель стремится к достижению такого состояния, при котором ему была бы обеспечена наибольшая прибыль при сложившихся рыночных условиях, т.е. прежде всего при имеющейся системе цен.

Наиболее простая модель оптимального поведения производителя в условиях совершенной конкуренции имеет следующий вид: пусть предприятие (фирма) производит один продукт в количестве y физических единиц. Если p – экзогенно заданная цена этого продукта и фирма реализует свой выпуск полностью, то она получает валовый доход (выручку) в размере:

R(y)=py.

В процессе создания этого количества продукта фирма несет производственные издержки в размере C(y). При этом естественно считать, что C¢(y)>0, т.е. издержки возрастают с увеличением объема производства. Также обычно полагают, что C¢¢(y)>0. Это означает, что дополнительные (маргинальные) издержки на производство каждой дополнительной единицы продукции возрастают по мере увеличения объема производства. Это предположение связано с тем, что при рационально организованном производстве, при малых объемах могут быть использованы лучшие машины и высококвалифицированные работники, которых уже не окажется в распоряжении фирмы, когда объем производства вырастет. На рис. 6.10 представлены типичные графики функций R(y) и C(y). Производственные издержки состоят из следующих составных частей:

1) материальные затраты C_m, в число которых входят расходы на сырье, материалы, полуфабрикаты и т.п.

Разность между валовым доходом и материальными затратами называется добавленной стоимостью (условно чистой продукцией)

VA = Z = R – C_m;

2) расходы на оплату труда C_l;

3) расходы, связанные с использованием, ремонтом машин и оборудования, амортизация, т.н. оплата «услуг капитала» C_k;

4) дополнительные расходы C_r, связанные с расширением производства, строительством новых зданий, подъездных путей, линий связи и т.д.

Совокупные производственные издержки:

C = C_m + C_l + C_k + C_r

Как уже было отмечено выше

С= С(y),

однако эта зависимость от объема выпуска (у) для разных видов издержек различна. А именно имеют место:

а) постоянные расходы C₀, которые практически не зависят от y, в т.ч. оплата административного персонала, аренда и содержание зданий и помещений, амортизационные отчисления, проценты за кредит, услуги связи и т.п.:

б) пропорциональные объему выпуска (линейные) затраты C₁, сюда входят материальные затраты C_m, оплата труда производственного персонала (часть C_l), расходы по содержанию действующего оборудования и машин (часть C_k) и т.п.

C₁ = ay,

где а – обобщенный показатель затрат указанных видов в расчете на одно изделие;

в) «сверхпропорциональные» (нелинейные) затраты С₂, в составе которых выступают приобретение новых машин и технологий т.е. затраты типа С_r), оплата сверхурочного труда и т.п. Для математического описания этого вида затрат обычно используется степенная зависимость:

С₂ = by^h (h > 1).

Таким образом, для представления совокупных издержек можно использовать модель

С(y) = C₀ + C₁ + C₂ = C₀ + ay + by^h. (2.1).

(Заметим, что условия C¢(y)>0, C¢¢(y)>0 для этой функции выполнены).

Рассмотрим возможные варианты поведения предприятия (фирмы) для двух случаев:

1) Предприятие имеет достаточно большой резерв производственных мощностей и не стремится к расширению производства, поэтому можно полагать, что C₂ = 0 и совокупные издержки являются линейной функцией объема выпуска:

С(y) = C₀ + ay

Прибыль составит:

П(y) = R – C = py – (C₀ + ay).

Очевидно, что при малых объемах выпуска 0 £ y £ y_w фирма несет убытки, т.к. П < 0.

Здесь y_w – точка безубыточности (порог рентабельности), определяемая соотношением П(y_w) = 0.

Если y > y_w, то фирма получает прибыль и окончательное решение об объеме выпуска зависит от состояния рынка сбыта производимой продукции (рис 6.10).

В этом случае имеются две точки безубыточности 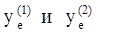, причем положительную прибыль фирма получит, если объем выпуска У , удовлетворяет условию .

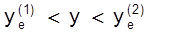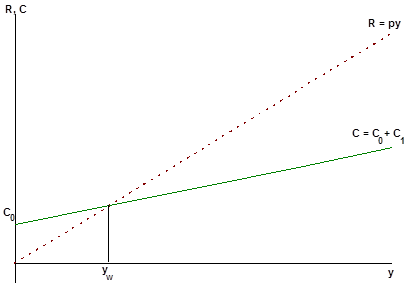
Рис. 6.10. Линии выручки и издержек предприятия

На этом отрезке в точке 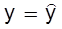достигается наибольшее значение прибыли, таким образом, существует оптимальное решение задачи о максимизации прибыли. В точке А, соответствующей издержкам при оптимальном выпуске, касательная к кривой издержек С параллельна прямой линии дохода R.

Следует заметить, что окончательное решение фирмы также зависит от состояния рынка, но с точки зрения соблюдения экономических интересов, ей следует рекомендовать оптимизирующее значение выпуска (рис. 6.11).

В общем случае, когда С(у) является нелинейной возрастающей и выпуклой вниз функцией (т.к. C¢(y)>0 и C¢¢(y)>0) объема выпуска, ситуация полностью аналогична той, которая рассмотрена в пункте 2. По определению, прибылью считается величина П(y) = R(y) – C(y).

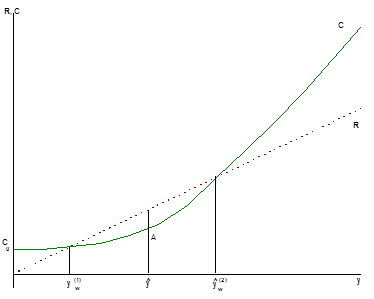
Рис 6.11. Оптимальный объем выпуска

Точки безубыточности 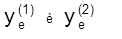, определяются из условия равенства прибыли нулю, а максимальное ее значение достигается в точке 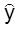, которая удовлетворяет уравнению:

П¢( 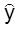) = 0 или R¢( 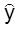) – C¢( 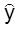) = 0.

Таким образом, оптимальный объем производства характеризуется тем, что в этом состоянии маргинальный валовый доход (R¢(y)) в точности равен маргинальным издержкам C¢(y).

В самом деле, если y < 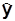, то R¢(y) > C¢ (y), и тогда следует увеличить выпуск продукции, поскольку ожидаемый дополнительный доход превысит ожидаемые дополнительные издержки. Если же y > 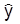, то R¢(y) < C¢(y), и всякое увеличение объема уменьшит прибыль, поэтому естественно рекомендовать уменьшить объем производства и придти в состояние y = 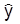(рис. 6.12).

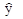
Рис. 6.12. Точка максимума прибыли и зона безубыточности:

(*).

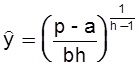Нетрудно видеть, что при увеличении цены (р) оптимальный выпуск
(а также прибыль) увеличиваются, т.е.

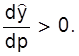
Это верно также и в общем случае, т.к.

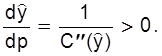
Пример. Фирма производит сельскохозяйственные машины в количестве у штук, причем объем производства в принципе может изменяться от 50 до 220 штук в месяц. При этом естественно увеличение объема производства потребует увеличения затрат, как пропорциональных так и сверхпропорциональных (нелинейных), поскольку потребуется приобрести новое оборудование и расширить производственные площади.

В конкретном примере будем исходить из того, что общие издержки (себестоимость) на производство продукции в количестве у изделий выражаются формулой:

C(y) = 1000 + 20y + 0.1y² (тыс. руб.)

Это означает, что постоянные издержки C₀ = 1000(т. руб.) пропорциональные затраты C₁ = 20y, т.е. обобщенный показатель этих затрат в расчете на одно изделие равена = 20тыс. руб.; а нелинейные затраты составят C₂ = 0.1y² (b = 0.1).

Приведенная формула выше для издержек является частным случаем общей формулы, где показатель h=2.

Для нахождения оптимального объема производства воспользуемся формулой точки максимума прибыли (*), согласно которой имеем:

.

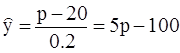Совершенно очевидно, что объем производства, при котором достигается максимальная прибыль, весьма существенно определяется рыночной ценой изделия Р.

В приводимой далее таблице, представлены результаты расчета оптимальных объемов при различных значениях цены от 40 до 60 тыс. рублей за изделие.

В первом столбце таблицы фигурируют возможные объемы выпуска у, второй столбец содержит данные о полных издержках С(у), в третьем столбце представлена себестоимость в расчете на одно изделие:

.

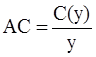Четвертый столбец характеризует значения указанных выше маргинальных издержек МС, которые показывают, во сколько обходится производство одного дополнительного изделия в данной ситуации. Нетрудно заметить, что маргинальные издержки возрастают по мере роста производства, что хорошо согласуется с положением, высказанным в начале этого параграфа. При рассмотрении таблицы следует обратить внимание на то, что оптимальные объемы находятся точно на пересечении строки (маргинальные издержки – МС) и столбца (цена – Р) с равными их значениями, что совершенно аккуратно соотносится с правилом оптимальности, установленным выше.

Проведенный выше анализ относится к обстановке совершенной конкуренции, когда производитель не может повлиять своими действиями на систему цен, и поэтому цена Р на товар У выступает в модели производителя как экзогенная величина.

Таблица 6.1