Приближение функций
Рассмотрим задачи, в которых требуется найти способ приближенного вычисления значения функции в заданной точке. Эти задачи возникают в тех случаях, когда прямое вычисление данной функции у = f(x)для произвольного аргумента невозможно или слишком трудоемко.
Например, функция f(x)определяется как решение сложной задачи. Здесь могут быть известны некоторые свойства функции у = f(x),например, непрерывность и дифференцируемость.
Даже если функция легко вычисляется, может возникнуть необходимость ее замены, например, при вычислении некоторых определенных интегралов или специальных функций математической физики (ниже будут приведены примеры). В этом случае вместо подынтегральной функции нужно подобрать другую функцию, от которой интеграл легко вычисляется. Разумеется, новая функция должна быть приближенно равна в некотором смысле подынтегральной функции.
Если значения функции определяются в результате дорогостоящих экспериментов, могут быть найдены ее значения только в некоторых точках, а для вычисления значения в произвольной точке требуется приближенный метод. При этом может быть известен вид функции, но неизвестны параметры, входящие в определение функции. В этом случае задача сводится к определению параметров известной функции.
Аппроксимацией(приближением) функции f(x)называется нахождение такой функции g(x)(аппроксимирующей функции),которая была бы близка заданной. Критерии близости функций могут быть различны.
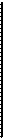 В том случае, когда приближение строится на дискретном наборе точек (xi, yi), i = 1, 2, ... , n, аппроксимацию называют точечнойили дискретной.
В том случае, когда приближение строится на дискретном наборе точек (xi, yi), i = 1, 2, ... , n, аппроксимацию называют точечнойили дискретной.
При точечной квадратичной аппроксимациипараметры а1, а2, ... , ат аппроксимирующей функции g = g(x, а1, а2, ... , ат), т £ п,определяются из условия
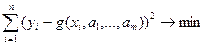 .
.
Если аппроксимация проводится на непрерывном множестве точек (отрезке), она называется непрерывнойили интегральной.
При интегральной квадратичной аппроксимациифункции у = f(х) на отрезке [а, b] параметры аппроксимирующей функции g(x, а1, а2,... , аm) определяются из условия
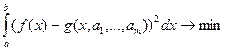 .
.
Примером непрерывной аппроксимации может служить использование конечного числа слагаемых разложения функции в ряд Тейлора, т. е. замена функции многочленом.
Наиболее часто встречающимся видом точечной аппроксимации на дискретном наборе из (n+1)-й точки (xi, yi), i = 0, 1, ... , п является интерполяциямногочленом n-го порядка Рп(х),коэффициенты которого определяются из условий
yi = Pn(xi), i = 0, 1, ... , п.
Применяя интерполяционный многочлен, можно вычислить значения функции f(x)между узлами (провести интерполяцию в узком смысле),а также определить значение функции за пределами заданного интервала (провести экстраполяцию).Следует иметь в виду, что погрешность экстраполяции может быть велика.
В том случае, когда интерполяционный многочленедин для всей области интерполяции, говорят, что интерполяция глобальная.Если между различными узлами интерполяционные многочлены различны, говорят о кусочнойили локальной интерполяции.Простейшим случаем локальной интерполяции является кусочно-линейная интерполяция, когда в качестве интерполяционной функции выбирается полином первой степени, т.е. узловые точки соединяются отрезками прямой.
Интерполяция
Под задачей интерполирования,или интерполяциипринято понимать следующую:
Пусть известны значения yi функции f(x)в точках хi i = 0, 1,..., п,называемых узлами интерполяции.Требуется найти такую функцию F(x)(интерполирующая функция),значения которой в узлах интерполяции совпадают со значениями f(x):
F(xi) = yi, i = 0,l, ... , n. (4.1)
Предполагается, что интерполирующая функция F(x)зависит от конечного числа параметров, которые находят из условий (4.1). Если зависимость интерполирующей функции F(x)от параметров линейна, то говорят о линейной интерполяции,в противном случае – о нелинейной интерполяции.В последнем случае нахождение параметров из системы (4.1) может быть трудной задачей.
Формула у = F(x)называется интерполяционнойи используется для вычисления значения функции f(x)в точке х,не совпадающей с узлами интерполяции. Эта операция называется интерполированием(интерполяцией) функции.При этом, если точка х не принадлежит отрезку [a, b], a = min(x0, х1,... , хп), b = mах(x0, х1,... , хп),то говорят об экстраполировании функции.
Часто в качестве интерполирующей функции используется многочлен такого порядка Рп(х)(интерполяционный многочлен),удовлетворяющий условию
yi = Pn(xi), i = 0, l,..., п. (4.2)
Так как многочлен n-го порядка определяется своими коэффициентами, то число параметров равно n +1 и условия (4.2) представляют систему линейных уравнений.
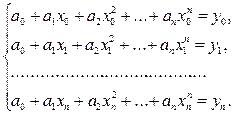 (4.3)
(4.3)

 Определителем системы (4.3) является определитель Вандермонда
Определителем системы (4.3) является определитель Вандермонда
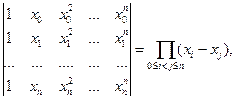 (4.4)
(4.4)
который отличен от нуля, если среди узлов интерполяции нет совпадающих. Отсюда следует, что задача построения интерполяционного многочлена разрешима и существует единственный интерполяционный многочлен, удовлетворяющий условиям (4.2). Как увидим ниже, формы записи интерполяционного многочлена могут быть разными. Отметим, что задача отыскания произвольного многочлена,удовлетворяющего условиям (4.2), некорректна. Если степень многочлена меньше п,то такого многочлена не существует, но если больше п,то таких многочленов бесконечное множество.
4.1.Интерполяционные формулы Ньютона
Пусть узлы интерполяции распределены на отрезке равномерно хi = а + ih, i = 0, 1, ... , п.Обозначим шаг изменения переменной х через Dх = h.
Введем сначала понятия конечной разностии обобщенной степени,которые используются для записи интерполяционной формулы Ньютона.
Первой конечной разностьюфункции у = f(x)называется выражение
Dу = f(x + Dх) – f(x). (4.5)
Конечная разность второго порядкаопределяется формулой
D2у = D(Dy)= D[f(х + Dх) - f(х)] = f(x + 2Dх) - 2 f(х + Dх) + f(x). (4.6)
Используя формулу бинома Ньютона, можно вывести формулу конечной разности п-го порядка:
Dnу = D(Dn-1y)= f(х + nDх) - 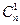 f[х + (n - 1)Dx] +
f[х + (n - 1)Dx] + 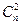 f[x + (n – 2)Dх] - ...+ (-1)n f(x), где
f[x + (n – 2)Dх] - ...+ (-1)n f(x), где 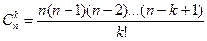 . (4.7)
. (4.7)
Справедливо утверждение: конечная разность(n+1)-го порядка многочлена п-го порядка равна нулю.
Пусть функция f(x)задана своими значениями yi = f(xi)в равноотстоящих точках xi = х0 + ih, i = 0, 1,..., п.
Таблица конечных разностейфункции f(х) записывается в одной из двух форм: горизонтальной или диагональной таблицы разностей. Так как конечная разность использует 2 значения, столбец Dyi содержит п значений, D2yi – на одно значение меньше и т. д. Если задано п +1 значений функции, то таблица конечных разностей содержит п столбцов, причем последний столбец содержит только одно значение. Общий вид горизонтальной таблицы, конечных разностейприведен в табл. 1.
Таблица 1
| xi | yi | Dyi | D2yi | D3yi | ... | Dn-1yi | Dnyi |
| x0 | y0 | Dy0 | D2y0 | D3y0 | ... | Dn-1y0 | Dny0 |
| x1 | y1 | Dy1 | D2y1 | D3y1 | ... | Dn-1y1 | |
| ... | ... | ... | ... | ... | ... | ||
| xn-2 | yn-2 | Dyn-2 | D2yn-2 | ||||
| xn-1 | yn-1 | Dyn-1 | |||||
| xn | yn |
Обобщенной степенью п-го порядкачисла х называется произведение
x[n] = x(x - h)(x -2h)(x - 3h)...[x - (n - 1)h], (4.8)
где h = const, а для n = 0 полагают x(0) = 1.
Найдем конечные разности для обобщенной степени:
Dх[n] = (х + h)(n) - x(n) = (x + h)x(x - h)(x -2h)...[x - (n - 2)h] - x(x - h)(x -2h)...[x - (n - 1)h] = x(x - h)(x -2h)(x - 3h)...[x - (n - 2)h]{( x + h) - [x - (n - 1)h]} = nh x[n - 1]
Мы получили следующую формулу:
Dх[n] = nh x[n - 1] (4.9)
Пользуясь методом математической индукции, можно вывести и общую формулу
Dkх[n] = n(n -1)...[n -(k - 1)] h kx[n - k]. (4.10)
Выведем первую интерполяционную формулу Ньютона. Найдем многочлен Рп(х), удовлетворяющий условиям Рп(хi)= yi для i = 0, 1,..., n. Будем искать многочлен Рп(х)в следующем виде:
Pп(х)= а0 + a1(х – х0) + a2(x – x0)(x – x1) + ... + an(x – x0)(x – x1)...(x – xn) =
= а0 + a1(х – х0)[1] + a2(x – x0)[2] + ... + an(x – x0)[n].
Из условия Рп(х0)= y0 следует a0 = y0.
Найдем первую конечную разность многочлена Рп(х):
DРn(х) = a1h + 2hа2(x – x0)[1] + ... + nan(x – x0)[n-1].
Отсюда при х = х0получим DРn(х0) = a1h = Dy0, т.е. a1 = Dy0/h. Аналогично можно получить общую формулу коэффициентов многочлена Ньютона:
ak = 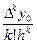 . (4.11)
. (4.11)
Теперь можно записать первую интерполяционную формулу Ньютона:
Pп(х)= y0 + 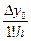 (х – х0)[1] +
(х – х0)[1] + 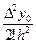 (x – x0)[2] + ... +
(x – x0)[2] + ... + 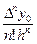 (x – x0)[n] (4.12)
(x – x0)[n] (4.12)
С помощью замены переменной q = (х - x0)/h первую интерполяционную формулу Ньютона можно представить в виде
Pп(х)= y0 + q 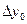 +
+ 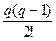
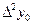 + ... +
+ ... + 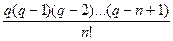
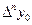 . (4.13)
. (4.13)
Аналогичными рассуждениями выводится вторая интерполяционная формула Ньютона:
Pп(х)= yn + 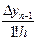 (х - хn) +
(х - хn) + 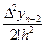 (x - xn)(x - xn-1) +...+
(x - xn)(x - xn-1) +...+ 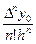 (x - xn)(x - xn-1)...(x - x1), (4.14)
(x - xn)(x - xn-1)...(x - x1), (4.14)
которая с помощью замены q = (х – xn)/h приводится к виду
Pп(х)= yn + q 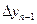 +
+ 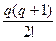
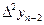 + ... +
+ ... + 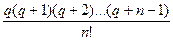
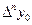 . (4.15)
. (4.15)
Первая интерполяционная формула Ньютона применяется для интерполирования вблизи начала таблицы (около х0), а вторая – для интерполирования вблизи конца таблицы (около хn).
4.2.Интерполяционная формула Лагранжа
Интерполяционные формулы Ньютона (4.12), (4.15) пригодны лишь для равноотстоящих узлов интерполирования. Рассмотрим интерполяционную формулу Лагранжа, которая применима при любом расположении узлов. Пусть дана система точек х0, х1, ..., хn, принадлежащих некоторому отрезку [а, b], и известны соответствующие значения функции yi = f(xi).Найдем многочлен Ln(x),удовлетворяющий условиям Ln(хi) = yi.
При построении многочлена Лагранжа используются многочлены n-й степени рi(х), принимающие значение 1 в точке xi и нулевые значения в остальных узлах интерполяции xj, j ¹ i.Так как xj,при j ¹ i являются корнями многочлена рi(х), то справедливо разложение рi(х) на множители
рi(х) = Ci(х - х0)(х - х1)...(х - хi-1)(х - хi+1) ...(х - xn), i = 0, 1, ... , n.
Из условия pi(xi) = 1 находим значение константы Ci:
Ci= 1/(хi - х0)(хi - х1)...(хi - хi-1)(хi - хi+1) ...(хi - xn) и получаем выражение для многочленов pi(xi):
рi(х) = 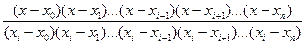 . (4.16)
. (4.16)
Интерполяционный многочлен Лагранжаимеет вид
Ln(x) = 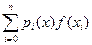 =
= 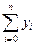 ×
× 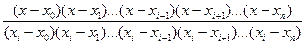 (4.17)
(4.17)
Формулу Лагранжа можно преобразовать так, чтобы упростить вычисления. Вынесем за знак суммы произведение
Пn+1(x) = (х - х0)(х – х1) ... (х - хn),
которое является многочленом степени п +1. Получим
Ln(x) = Пn+1(x) 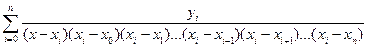 .
.
Теперь формулу Лагранжа можно записать в виде
Ln(x) = Пn+1(x) 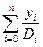 , (4.18)
, (4.18)
где Di = (хi - х0)(хi - х1)...(хi - хi-1)(x - xi)(хi - хi+1) ...(хi - xn).
Обратите внимание на то, что в произведении Di из n + 1 сомножителя вместо скобки (хi - xi)присутствует множитель (х – xi).
4.3.Остаточный член интерполяционной формулы Лагранжа
Для анализа погрешности интерполяции используется остаточный член интерполяционного многочлена Лагранжа
f(x) – Ln(x) = 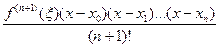 =
= 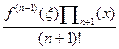 (4.19)
(4.19)
где x принадлежит отрезку [a, b], который определяется числами
а = min(x0, х1,..., хп, х), b = mах(x0, х1,..., хп, х). (4.20)
Формула (4.19) выводится с помощью функции
φ(х) = f(x) – Ln(x) – KПn+1(x),
где параметр К выбирается из условия φ(х) = 0:
K=(f(x) – Ln(x))/ Пn+1(x).
Пусть функция f(x)имеет непрерывную производную (n +1)-го порядка. Тогда φ(х) имеет п +2 корня х0, х1,..., xn, x и по теореме Ролля производная φ'(x) имеет п +1 корень, вторая производная φ"(х) равна нулю в п точках, а производная (п +1)-го порядка φ(n + 1)(х) равна нулю в некоторой точке x,из отрезка [а, b],который определяется условиями (4.20). Далее
φ(n + 1)(х) = f(n+1)(х) – К(п +1)!,
так как производная (n+1)-го порядка от многочлена Lп(х)равна нулю, а у многочлена Пn+1(x) старший член равен xn+1и производная (n +1)-го порядка многочлена Пn+1(x) равна (n +1)!.
Из условия φ(n + 1)(x) = f(n+1)(x) - К(п +1)! = 0 следует
K = f(n+1)(x)/(п +1)!,
а из равенства φ(х) = f(x) - Ln(x) – KПn+1(x)= 0 следует (4.19).
4.4.Равномерное приближение функции.Многочлены Чебышева
Определение 4.1. Многочлен Рп(х) равномерно приближает на отрезке [а, b] функцию f(x) с точностью до ε, если выполняется неравенство
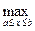 | f(x) – Pn(x)| £ ε. (4.21)
| f(x) – Pn(x)| £ ε. (4.21)
Приведем без доказательства теорему Вейерштрасса.
Теорема 4.1.Если функция f(x)непрерывна на отрезке [а, b],то для любого ε > 0 найдется многочлен Рn(х) достаточно высокой степени n, который равномерно приближает на отрезке [а, b]функцию f(x)с точностью до ε, т. е. выполняется (4.21).
Определение 4.2. Многочлен Рп(х)называется многочленом наилучшего приближениядля функции f(x)на отрезке [а, b],если для любого многочлена Qn(x) степени n выполняется неравенство
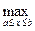 | f(x) – Pn(x)| £
| f(x) – Pn(x)| £ 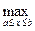 | f(x) – Qn(x) |. (4.22)
| f(x) – Qn(x) |. (4.22)
Многочлены Чебышеваопределяются рекуррентными формулами
Т0(х) = 1, Т1(х) = х, Tn+1(x) = 2хТп(х)- Тп-1(х)при n ³ 1. (4.23)

 Выпишем многочлены Чебышева Тп(х) для п = 2, 3, 4, 5:
Выпишем многочлены Чебышева Тп(х) для п = 2, 3, 4, 5:
Т2(х)= 2хТ1(х) – T0 = 2х2 – 1,
Т3(х) = 2хТ2(х)– T1 = 4х3 – 3х,
Т4(х) = 8х4 – 8х2 + 1,
Т5(х) = 16х5 – 20х3 + 5х.
Старший коэффициент многочлена Тn(х), т. е. коэффициент при хп,равен 2n-1.
Справедливо представление многочленов Чебышева через тригонометрические функции
Tn(x)= cos(n×arccos х), при п ³ 0. (4.24)
Поэтому |Тn(х)| £ 1 для | х | £ 1. (4.25)
Корни многочлена Чебышева принадлежат отрезку [-1; 1]:
xk = 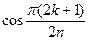 , k = 0, 1, ... , n - 1. (4.26)
, k = 0, 1, ... , n - 1. (4.26)
Многочлены Чебышева Тп(х) с четными индексами являются четными функциями, а с нечетными – нечетными функциями.
Многочлены Чебышева Тn(х) обладают следующим замечательным свойством. Если умножить Тп(х)на 21-n, получится многочлен, наименее уклоняющийся от нуляна отрезке [-1; 1].
Теорема 4.2. Если Рп(х)– произвольный многочлен степени п со старшим коэффициентом 1, справедливо неравенство
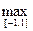 | Pn(x) | ³
| Pn(x) | ³ 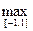 | 21-n×Tn(x) | =
| 21-n×Tn(x) | = 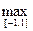
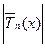 = 21-n , (4.27)
= 21-n , (4.27)
где 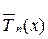 = 21-n×Tn(x).
= 21-n×Tn(x).
В некоторых учебниках по численным методам многочленом Чебышева называется многочлен
Тn(х) = 21-n×Tn(x), наименее уклоняющийся от нуляна отрезке [-1; 1].
Поясним смысл теоремы 4.2 на примерах.
Если п = 2, то теорема 4.2 утверждает, что наибольшее значение любой квадратной функции вида х2 + рх + q на отрезке [-1; 1] не меньше 21-2 = 0,5.
Наибольшее значение любого многочлена вида х3 + рх2 + qx + r на отрезке [-1; 1] не меньше 21-3 = 0,25.
Среди всех квадратных функций вида х2 + рх + q наименее уклоняющимся от нуля на отрезке [-1; 1] многочленом является функция
21-2×T2(x) = х2 - 0,5.
Среди всех многочленов вида х3 + рх2 + qx + r наименее уклоняющимся от нуля на отрезке [-1; 1] является многочлен
21-3Т3(х)= (4х3 - 3х)/4 = х3 - 0,75х.
Для произвольного отрезка [а, b]многочлен со старшим коэффициентом 1, наименее уклоняющийся от нуля, получается из 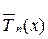 заменой
заменой
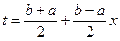 .
.
Этот многочлен имеет вид
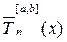 = (b - a)n×21-2n×Tn
= (b - a)n×21-2n×Tn 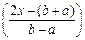
Корнями многочлена 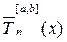 являются точки
являются точки
xk = 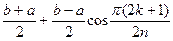 , k = 0, 1, ... , n - 1. (4.29)
, k = 0, 1, ... , n - 1. (4.29)
Многочлены Чебышева используются для минимизации погрешности интерполяционной формулы за счет оптимального выбора узлов интерполяции. В формуле остаточного члена (4.19) у многочлена Пn+1(х)старший коэффициент равен 1. Для минимизации погрешности интерполяционной формулы для функции f(x) на отрезке [а, b]нужно взять в качестве узлов интерполяции точки
xk = 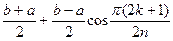 , k = 0, 1, ... , n. (4.30)
, k = 0, 1, ... , n. (4.30)
являющиеся корнями многочлена 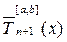 . Тогда погрешность интерполяции оценивается неравенством
. Тогда погрешность интерполяции оценивается неравенством
| f(x) – Ln(x)|£ 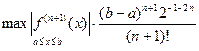 . (4.31)
. (4.31)
4.5. Интерполяция сплайнами
Пусть задана таблица значений функции yi в узлах х0 < х1 < ... < хп.Обозначим hi = xi – xi-1, i = 1, 2, ... , п.
Сплайн– гладкая кривая, проходящая через заданные точки (хi, yi), i = 0, 1, ... , п. Интерполяция сплайнами заключается в том, что на каждом отрезке [хi-1, xi]используется многочлен определенной степени. Наиболее часто применяется многочлен третьей степени, реже – второй или четвертой. При этом для определения коэффициентов многочленов используются условия непрерывности производных в узлах интерполяции.
Интерполяция кубическими сплайнамипредставляет собой локальную интерполяцию, когда на каждом отрезке [хi-1, xi], i = 1, 2, ... , п применяется кубическая кривая, удовлетворяющая некоторым условиям гладкости, а именно, непрерывности самой функции и ее первой и второй производных в узловых точках. Использование кубической функции вызвано следующими соображениями. Если предположить, что интерполяционная кривая соответствует упругой линейке, закрепленной в точках (хi, yi),то из курса сопротивления материалов известно, что эта кривая определяется как решение дифференциального уравнения f(IV)(x) = 0 на отрезке [хi-1, xi](для простоты изложения мы не рассматриваем вопросы, связанные с физическими размерностями). Общим решением такого уравнения является многочлен 3-й степени с произвольными коэффициентами, который удобно записать в виде
Si(x) = аi + bi(х - xi-1) + сi(x - xi-1)2+ di(x - xi-1)3,
хi-1 £ х £ хi, i = 1, 2, ... , п.(4.32)
Коэффициенты функций Si(x)определяются из условий непрерывности функции и ее первой и второй производных во внутренних узлах xi, i = 1, 2,..., п - 1.
Из формул (4.32) при х = хi-1 получим
Si(xi-1) = yi-1 = ai, i = 1, 2,..., п,(4.33)

 а при х = хi
а при х = хi
Si(xi) = аi + bihi + сihi2+ dihi3,(4.34)
i = 1, 2,..., n.
Условия непрерывности интерполяционной функции записываются в виде Si(xi) = Si-1(xi), i = 1, 2, ... , n - 1 и из условий (4.33) и (4.34) следует, что они выполнимы.
Найдем производные функции Si(x):
S'i(x) = bi + 2сi(х - xi-1) + 3di(х – xi-1)2,
S"i(x) = 2ci + 6di(x - xi-1).
При x = xi-1, имеем S'i(xi-1) = bi, S" (xi-1) = 2сi, а при х = хi получим
S'i(xi) = bi + 2сihi + 3dihi2, S" (xi) = 2сi + 6dihi.
Условия непрерывности производных приводят к уравнениям
S'i(xi) = S'i+1(xi) Þ bi + 2сihi + 3dihi2 = bi+1,
i = l, 2,... , п - 1. (4.35)
S"i (xi) = S"i+1(xi) Þ 2сi + 6dihi = 2ci+1,
i = l, 2,..., n - 1. (4.36)
Всего имеем 4n – 2 уравнений для определения 4n неизвестных. Чтобы получить еще два уравнения, используют дополнительные краевые условия, например, требование нулевой кривизны интерполяционной кривой в концевых точках, т. е. равенства нулю второй производной на концах отрезка [а, b] а = х0, b = хn:
S"1(x0) = 2c1 = 0 Þ с1 = 0,
S"n(xn) = 2сn + 6dnhn = 0 Þ сn + 3dnhn = 0. (4.37)
Систему уравнений (4.33)–(4.37) можно упростить и получить рекуррентные формулы для вычисления коэффициентов сплайна.
Из условия (4.33) имеем явные формулы для вычисления коэффициентов ai:
ai = yi-1, i= 1,..., n. (4.38)
Выразим di через ci с помощью (4.36), (4.37):
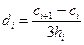 ; i = 1, 2,...,n;
; i = 1, 2,...,n; 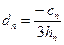 .
.
Положим сn+1= 0, тогда для di получим одну формулу:
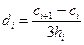 , i = 1, 2,...,n. (4.39)
, i = 1, 2,...,n. (4.39)
Подставим выражения для аi и di в равенство (4.34):
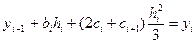 , i = 1, 2,..., n.
, i = 1, 2,..., n.
и выразим bi, через сi:
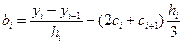 , i = 1, 2,..., n. (4.40)
, i = 1, 2,..., n. (4.40)
Исключим из уравнений (4.35) коэффициенты bi и di с помощью (4.39) и (4.40):
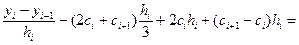
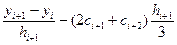 ,
,
i = 1, 2,..., n -1.
Отсюда получим систему уравнений для определения сi:
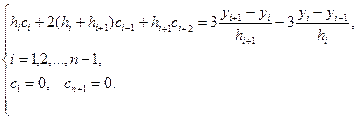 (4.41)
(4.41)
Система уравнений (4.41) может быть переписана в виде
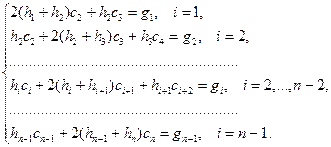 (4.42)
(4.42)
Здесь введено обозначение
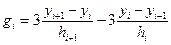 , i =1, 2,..., n - 1.
, i =1, 2,..., n - 1.


 Решим систему уравнений (4.42) методом прогонки. Из первого уравнения выразим с2через с3:
Решим систему уравнений (4.42) методом прогонки. Из первого уравнения выразим с2через с3:
c2 = a2c3 + b2, 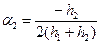 ,
, 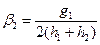 . (4.43)
. (4.43)
Подставим (4.43) во второе уравнение (4.42):
h2(a2c3 + b2) + 2(h2 + h3)c3 + h3c4 = g2,
и выразим с3 через с4:
с3 = a3с4 + b3, 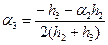
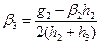 (4.44)
(4.44)
Предполагая, что сi-1= ai-1ci + bi-1 из i-го уравнения (4.42) получим
ci = aiсi+1 + bi
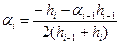 , i = 3,..., n – 1, an = 0, (4.45)
, i = 3,..., n – 1, an = 0, (4.45)
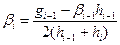 , i = 3,..., n.
, i = 3,..., n.
Сформулируем алгоритм интерполяции с помощью кубического сплайна.
Исходные данные: значения функции у0, у1,..., уп в узлах х0, х1,..., хп (х0 < х1< ... < хn).
0. Вычислим значения hi и gi:
hi = xi – xi-1 i = 1, 2,..., n,
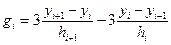 , i =1, 2,..., n - 1. (4.46)
, i =1, 2,..., n - 1. (4.46)
1. Прямой ход прогонки для вычисления коэффициентов ci. Вычислим коэффициенты прогонки ai и bi:
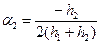 ,
, 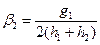 ,
,
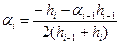 , i = 3,..., n – 1, an = 0, (4.47)
, i = 3,..., n – 1, an = 0, (4.47)
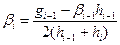 , i = 3,..., n.
, i = 3,..., n.
2. Обратный ход прогонки для вычисления коэффициентов сi. Вычислим коэффициенты ci:
cn+1 = 0,
ci = aiсi+1 + bi, i = n, n -1,..., 2, (4.48)
c1 = 0.
3. Вычисление коэффициентов аi, bi, di:
ai = yi-1, 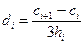
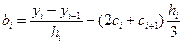 , (4.49)
, (4.49)
i = 1, 2,..., n.
4. Вычисление значения функции с помощью сплайна. Для этого найти такое значение i,что данное значение переменной х принадлежит отрезку [xi-1, xi] и вычислить
Si(x) = аi + bi(х - xi-1) + сi(x - xi-1)2+ di(x - xi-1)3. (4.50)
4.6. Аппроксимация. Метод наименьших квадратов
Наиболее распространенным методом аппроксимации экспериментальных данных является метод наименьших квадратов.
Пусть заданы значения функции yi,соответствующие значениям xi, i = 1, 2, ... , п. Предположим, что аппроксимирующая функция g(x)зависит от т параметров  g = g(x, a1, a2, ... , am), т £ п.При точечной квадратичной аппроксимации параметры а1, а2,... , ат аппроксимирующей функции определяются из условия минимума суммы квадратов отклонений значений аппроксимирующей функции от заданных значений функции:
g = g(x, a1, a2, ... , am), т £ п.При точечной квадратичной аппроксимации параметры а1, а2,... , ат аппроксимирующей функции определяются из условия минимума суммы квадратов отклонений значений аппроксимирующей функции от заданных значений функции:
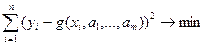 ,(4.51)
,(4.51)
Вид функции g(x, a1, а2, ... , ат)определяется особенностями решаемой задачи, например, физическими соображениями, если проводится аппроксимация результатов физического эксперимента.
Если аппроксимирующая функция линейно зависит от параметров, то метод наименьших квадратов приводит задачу ее определения к системе линейных уравнений.
Наиболее часто применяются аппроксимации прямой линией (линейная регрессия),полиномом (полиномиальная регрессия), линейной комбинацией линейно независимых функций.
Рассмотрим применение метода наименьших квадратов для определения параметров функции g(x, a1, а2, ... , ат)при аппроксимации линейной комбинацией линейно независимых функций:
g(x, a1, а2, ... , ат) = a1φ1(x) + a2φ2(x) +...+ amφm(x).(4.52)
Тогда условие (4.51) имеет вид
S(a1,...,am) = 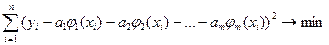 . (4.53)
. (4.53)
Минимум квадратичной функции существует; необходимым условием его существования является равенство нулю частных производных
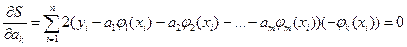 , k = 1, ... ,m.(4.54)
, k = 1, ... ,m.(4.54)
Из (4.54) получим систему уравнений метода наименьших квадратов необходимого условия существования минимума:
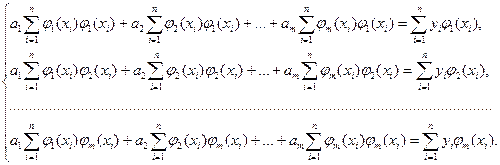 (4.55)
(4.55)
При линейной аппроксимирующей функции
g(x, а0, а1) = а0 + а1х (4.56)
система (4.55) имеет вид
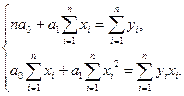 (4.57)
(4.57)
Аналогично можно получить систему уравнений для определения параметров полиномиальной регрессии:
g(x, а0, ... , ат) = а0 + а1х + ... + атхт.(4.58)
В этом случае получим систему из т +1 уравнения с т +1 неизвестным
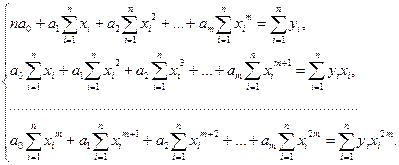 (4.59)
(4.59)
Если зависимость аппроксимирующей функции от параметров нелинейна, то для определения параметров приходится решать нелинейные задачи. Иногда удается с помощью преобразований вместо функции с нелинейной зависимостью от параметров рассматривать функцию 

 с линейной зависимостью от параметров.
с линейной зависимостью от параметров.
| <== предыдущая лекция | | | следующая лекция ==> |
| Вычислительные методы линейной алгебры | | | Численное дифференцирование |
Дата добавления: 2020-08-31; просмотров: 1079;











