Спектральный анализ детерминированных гармонических сигналов с использованием ДПФ

10.2.1Структура спектрального анализатора с использованием ДПФ

Спектральный анализ сигналов может быть выполнен с помощью дискретного преобразования Фурье (ДПФ). Для анализа используется взвешенная входная последовательность 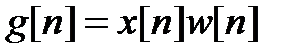, которая определяется как произведение дискретного сигнала x[n] на некоторую весовую функцию w[n] на конечном интервале N.

g[n]

´

Д П Ф   (БПФ)

w[n]

x[n]

. . .

g[0]

g[1]

g[R-1]

. . .

Канал 0

Канал 1

Канал R-1

Рисунок 10.1 – оценка спектра с использованием ДПФ

10.2.2Частотная характеристика одного канала ДПФ

Рассмотрим формулу ДПФ в виде линейной дискретной свертки:

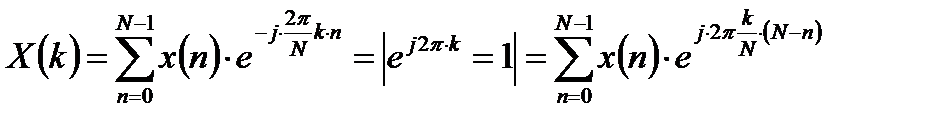. (10.1)

Импульсная характеристика одного канала ДПФ определяется выражением:

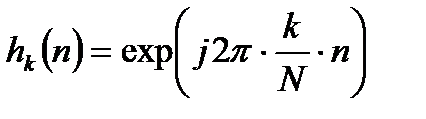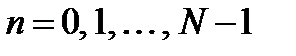, . (10.2)

Передаточная функция такого фильтра является z-преобразованием от импульсной характеристики:

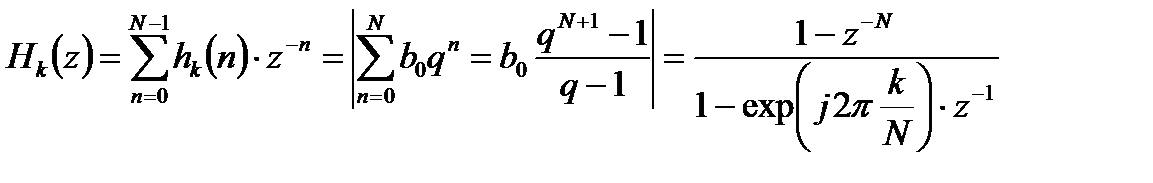. (10.3)

Частотную характеристику фильтра получим в результате использования подстановки :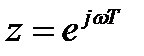

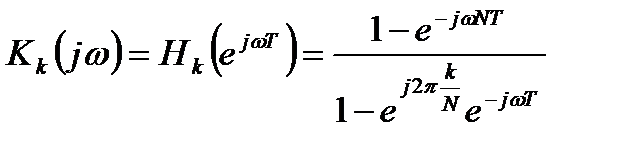. (10.4)

После выполнения преобразований АЧХ такого фильтра примет следующий вид:

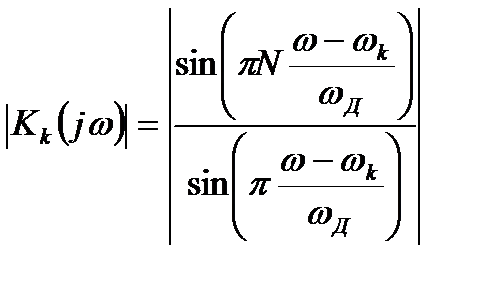, (10.5)

где 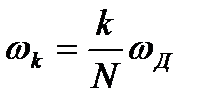- частота настройки k-ого фильтра;

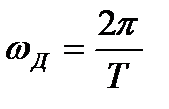- частота дискретизации входного сигнала.

АЧХ одного канала ДПФ имеет максимальный уровень боковых лепестков, равный:

.

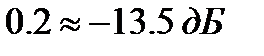Ширина главного лепестка АЧХ определяет разрешающую способность спектрального анализа и равна:

.

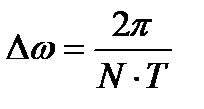График АЧХ одного из каналов ДПФ приведен на рисунке 10.2.

Рисунок 10.2 – АЧХ одного из каналов ДПФ

10.2.3Явление растекания спектра

При вводе понятия ДПФ предполагалось, что анализируемая последовательность периодически продолжается за пределами окна анализа. Если значения начальных и конечных отсчетов сигнала сильно отличаются, то при периодическом продолжении возникают сильные скачки на стыках окон. Это приводит к явлению растекания спектра.

Примерные графики дискретного гармонического сигнала и модуля его спектра для случаев целого и нецелого числа периодов в пределах окна анализа приведены на рисунке 10.3.

Рисунок 10.3 – дискретный гармонический сигнал и его спектры

Поясним растекание спектра с использованием спектров дискретизированных синусоид. Спектры дискретизированных сигналов являются периодическими непрерывными функциями. В случае целого числа периодов синусоиды в пределах окна анализа все дискретные значения отсчетов ДПФ попадают на границы между боковыми лепестками. При нецелом числе периодов синусоиды в пределах окна анализа этого не происходит и наблюдается явление растекания спектра.

Рисунок 10.4 – спектры дискретизированных гармонических сигналов

10.2.4Использование весовых функций

Для уменьшения явления растекания спектра при использовании ДПФ применяют весовые функции. В этом случае перед расчетом ДПФ входной сигнал 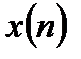умножается на весовую функцию 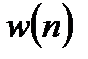, спадающую по краям:

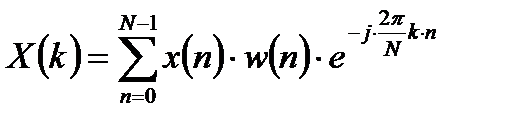. (10.7)

Это приводит к ослаблению эффектов, связанных со скачком сигнала при его периодическом продолжении.

Использование весовой функции приводит к уменьшению уровня боковых лепестков частотных характеристик каналов ДПФ.

Платой за уменьшение уровня боковых лепестков является расширение центрального лепестка частотной характеристики: рисунок 10.5.

Рисунок 10.5 – АЧХ одного из каналов ДПФ до и после использования весовой обработки

Наиболее известны следующие весовые функции:

· Хэмминга: 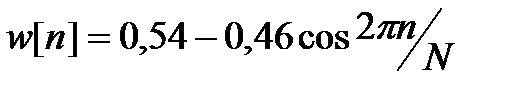, d_бл= - 43 дБ;

Литература

1. Сергиенко А.Б. Цифровая обработка сигналов / А.Б. Сергиенко. – Спб.: Питер, 2003. - 608 с. (с. 262).