Показания стационарных нейтронных методов в сухих скважинах и имитаторах пластов

Зависимость показаний детектора от размера зонда Z и радиуса сухой сква­жины имеет вид:

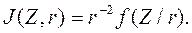(9.223)

Эта закономерность теоретически установлена для гамма-квантов [4] и экспериментально подтверждена для нейтронов [6] в связи с изучением поля точечного источника в полых цилиндрических каналах.

Свойства полей надтепловых и тепловых нейтронов определяются пространственным распределением быстрых, поэтому закономерность (9.223) необходимо учесть при анализе поля излучения в системе “сухая скважина - пласт”. С учетом уравнения (9.223) определение декремента пространственного спада α (1091) можно представить в виде:

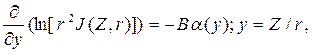(9.224)

где В – размерная константа, подлежащая определению.

Тогда выражения (110) и (117) [Н. Х.] примут вид:

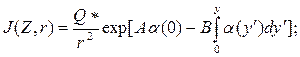(9.225)

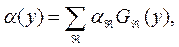(9.225')

где Q* - эффективная мощность источника нейтронов (учитывающая эффектив­ность детектора и вероятность избежать поглощения в процессах замедления и диффузии): α_k – соответственно обратная длина замедления (ННМ-нт) или обратная длина миграции (ННМ-т) в веществе k-й зоны; G_k – геометрический фактор (“ценность”) k-й зоны; А – размерная константа, подлежащая определению.

Рис.9.21. Схема базовой установки ИПП (по З. З. Ханипову). а – общий вид; б – имитатор пористого пласта. 1 – емкость с водой, 2 – ИПП, 3 – скважинный прибор, 4 – тренога с лебедкой, 5 – кабель, 6 – измерительное устройство,

В сухой скважине при отсутствии стальной колонны, глинистой корки и других промежуточных сред имеется лишь одна излучающая зона – пласт, геометрический фактор которого G=1. Поэтому обратная длина релаксации α в системе скважина – пласт совпадает с обратной длиной миграции нейтронов в пласте: α≡α(m), и выражение (9.225) упрощается:

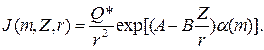(9.226)

Определим константы А и В. Зафиксируем радиус скважины r=a и найдем зонд нулевой чувствительности Z₀(a), который определяется условием

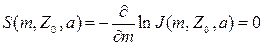. (9.227)

Отсюда вытекает соотношение между константами А и В

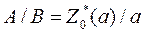(9.228)

и следует, что Z₀ не зависит от водородосодержания пласта m.

Для двух пластов с различным водородосодержанием m₁ и m₂ определим инверсионный зонд Z*, на котором дифференциация показаний равна единице:

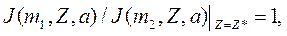(9.229)

Откуда

A/B=Z*(a)/a. (9.227')

На основании выражений (9.228) и (9.228') инверсионный зонд совпадает с зондом нулевой чувствительности.

Для определения константы В найдем декремент α(m,r) пространственного спада показаний. На основании уравнения (9.226) получим

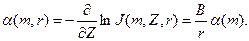(9.230)

Если радиус скважины r равен внешнему радиусу прибора r₀, то должно выполняться равенство α(m,r₀)= α(m) и, следовательно, B=r₀. Окончательно выражение (9.226) принимает следующий вид:

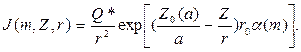(9.231)

Отсюда следует, что в сухих скважинах инверсия зависимости показаний от водородосодержания (пористости) m происходит не только с изменением длины зонда (при фиксированном диаметре скважины), но и с изменением диаметра скважины (при фиксированной длине зонда).