Погрешность округления

Так как в компьютере приходится прибегать к округлению чисел, то неизбежны погрешности округления. Если для представления мантиссы используется только n разрядов, то изображение числа разбивается на две части:

Aq= [m]qn+ [A0]qp-n,

где [A0]qp-n= A0 - "хвост" числа, не попавший в разрядную сетку.

В зависимости от того, как учитывается величина А0 в машинном изображении, существует несколько способов округления.

1. Отбрасывание А0. При этом относительная погрешность равна

окр = .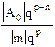

Так как q-1 |m| < 1; то 0 |A0| < 1, поэтому

окр = 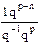= q-(n-1),

т.е. погрешность округления не зависит от величины самого числа, а зависит только от количества разрядов в машине для любой системы счисления.

2. Симметричное округление. При этом производится анализ величины А0. Принимая, что

\

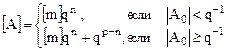При условии |A0| q-1производится прибавление единицы к младшему разряду мантиссы. Абсолютная погрешность при этом

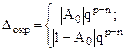
Максимально возможное значение модуля абсолютной погрешности равно 0,5qp-n , а относительная погрешность равна

окр 0,5qp-n/(mqp) = 0,5q-(n-1),

т.е. ошибка не превышает половины единицы младшего разряда. Способ симметричного округления наиболее часто применяют на практике.

3. Округление по дополнению. В этом случае для округления берется информация, содержащаяся в (n+1)-м разряде. При q = 2, если в (n+1)-м разряде содержится 1, в n-й разряд добавляется 1; если же там ноль, содержимое разрядов правее n-го отбрасывается.

Глава 5.