Оценка точности выполнения арифметических операций

Как уже неоднократно отмечалось, для представления чисел в любой форме в компьютере отводится конечная длина разрядной сетки. Поэтому числа, в общем случае, из-за неизбежных процедур округления, представляются с некоторой погрешностью. В связи с этим вычисления в компьютере выполня-ются с погрешностью, которая в некоторых случаях может существенно накапливаться.

Пусть величины А и В заданы с абсолютными погрешностями А и В:

А = [A] А, В = [B] В= где [A] и [B] - машинное представление чисел А и В. Тогда, как нам уже известно, относительные погрешности представления этих чисел будут равны:

A = A / |A| и B = B / |B|.

Можно показать, что относительная погрешность алгебраической суммы будет равна:

,

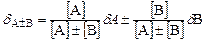относительная погрешность произведения:

AB = |A| + |B|,

а относительная погрешность частного:

A/B = |A| + |B|,

Из приведенных соотношений видно, что операция умножения и деления незначительно увеличивают относительную погрешность, а вычитание почти равных чисел может сильно ее увеличить. Действительно, если принять, что

= A B, а [A] мало отличается от [B], то

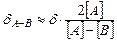
В связи с тем, что величина (А - В) в данном случае мала, а то А-В может быть достаточно большой величиной.

Из-за неизбежных погрешностей машинных вычислений может наблюдаться нарушение некоторых основных законов математики. Например, может не выполняться точно закон ассоциативности для умножения. Закон дистрибутивности, связывающий операции умножения и сложения, может значительно нарушаться, т.е. не будет строго выполняться равенство:

А х (В + С) = (А х В) + (А х С),

а отсюда может возникнуть ситуация, когда

2 х (А2+ В2) < (А + В)2.

Поэтому нужно очень тщательно оценивать конкретные условия вычислений и, при необходимости, переходить к представлению чисел с двойной точностью и принимать различные другие меры, чтобы в какой-то степени исключить влияние накопленной погрешности на результат вычислений.