Преобразования алфавитной информации
В наиболее общем виде преобразование алфавитной информации может быть следующим способом. Пусть даны два конечных алфавита 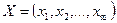 и
и 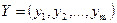 . Обозначим через
. Обозначим через 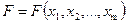 совокупность всех слов конечной длины в алфавите Х, через
совокупность всех слов конечной длины в алфавите Х, через 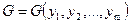 - совокупность всех слов конечной длины в алфавите Y. Если исходная информация записывается в алфавите Х, а конечная информация – в алфавите Y, то произвольное преобразование информации
- совокупность всех слов конечной длины в алфавите Y. Если исходная информация записывается в алфавите Х, а конечная информация – в алфавите Y, то произвольное преобразование информации 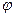 будет представлять собой не что иное, как отображение множества F в множестве G.
будет представлять собой не что иное, как отображение множества F в множестве G.
В дальнейшем мы будем рассматривать только детерминированные преобразования информации, при которых входное слово полностью определяет слово на выходе преобразователя. Т.о. требование детерминированности есть не что иное, как требование однозначностиотображения 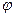 .
.
Целесообразно в общем случае считать 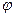 частичным отображением, т.е. задавать отображение
частичным отображением, т.е. задавать отображение 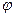 не обязательно на всем множестве F, а лишь на части этого множества. Введение частичных отображений позволяет вместо отображений одного множества слов в другое рассматривать лишь отображение таких множеств в себя. Для этой цели достаточно ввести объединенный алфавит
не обязательно на всем множестве F, а лишь на части этого множества. Введение частичных отображений позволяет вместо отображений одного множества слов в другое рассматривать лишь отображение таких множеств в себя. Для этой цели достаточно ввести объединенный алфавит 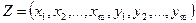 и множество
и множество 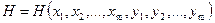 слов в этом алфавите. Ясно, что вместо отображения (или частичного отображения) множества F в множество G можно рассматривать частичное отображение множества Н в себя. Это частичное отображение будет определено для слов, состоящих только из букв
слов в этом алфавите. Ясно, что вместо отображения (или частичного отображения) множества F в множество G можно рассматривать частичное отображение множества Н в себя. Это частичное отображение будет определено для слов, состоящих только из букв 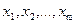 .
.
Однозначность отображения 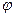 множества f в множество G не означает однозначности обратного отображения
множества f в множество G не означает однозначности обратного отображения 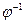 . Если же такая однозначность имеет место, то отображение
. Если же такая однозначность имеет место, то отображение 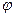 называется взаимнооднозначным, в этом случае отображение
называется взаимнооднозначным, в этом случае отображение 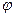 осуществляет эквивалентное преобразование информации.
осуществляет эквивалентное преобразование информации.
Пример 1 (зеркало) – эквивалентное. Пример 2 (сумма двух чисел) – не эквивалентное.
Преобразования, заключающиеся в замене каждой буквы исходного алфавита некоторой определенной комбинацией букв нового алфавита с фиксированной длиной, называются простейшими или побуквенными.
С помощью простейших эквивалентных преобразований, информацию, заданную в любом конечном алфавите, можно записать в алфавите, содержащем только 2 буквы. Это – стандартный двухбуквенный или двоичный алфавит.
Если число букв в исходном алфавите А – n, то число слов, отображающих буквы алфавита А в двоичный алфавит должно быть 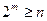 , где
, где 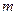 - разрядность (длина) слова. Такое преобразование называется двоичнымкодированием информации и оно неоднозначно. Т.о. при двоичных преобразованиях информации можно предполагать. Что как исходная, так и заключительная информация задана в некотором стандартном алфавите.
- разрядность (длина) слова. Такое преобразование называется двоичнымкодированием информации и оно неоднозначно. Т.о. при двоичных преобразованиях информации можно предполагать. Что как исходная, так и заключительная информация задана в некотором стандартном алфавите.
 Пример сведения сложного процесса преобразования информации к преобразованию слов в двоичном алфавите – распознавание рисунков.
Пример сведения сложного процесса преобразования информации к преобразованию слов в двоичном алфавите – распознавание рисунков.
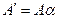
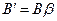
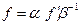 ,
, 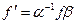 .
.
Дата добавления: 2016-07-18; просмотров: 1927;











