Умножение чисел, представленных в форме с плавающей запятой

При операции умножения чисел, представленных в форме с плавающей запятой их мантиссы умножаются, как числа с фиксированной запятой, а порядки складываются. В обоих случаях проверка на переполнение обязательна. Но, т.к. реально складываются характеристики чисел, то умножение выполняется по следующей формуле:

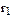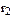A1 x A2 = m12 x m22 = (m1 x m2)2 ,

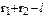где r1 + r2 - l - характеристика результата.

Знак ответа определяется обычным образом. Если ответ получился ненормализованный, то выполняются процедуры нормализации и округления ответа.

Напомним, что при реализации алгоритмов математических операций в формате с плавающей запятой каждый раз, когда осуществляется та или иная процедура, затрагивающая характеристики операндов или результата, производится контроль над переполнением и исчезновением порядка, т.е. контролируется условие

0 r rmax ,

где rmax = l + pmax .

Рассмотрим пример:

умножим числа с мантиссами m1 = 0,101 (5), m2 = 0,1 (2) и характеристиками

r1 = 1011, r2 = 1010, l = 1000, p1 = 3, p2 = 2, p = p1 + p2 = 5, r = r1 + r2 - l = 001011 + 001010 - 001000 = 001101 = 1310 m = m1 x m2 = 0,01010, необходимо нормализовать ответ. Для этого в данном случае сдвигаем мантиссу влево на 1 разряд и вычитаем 1 из p, получаем p = 4. В итоге имеем m = 0,10102, p = 410 = 01002, r = 1210 = 11002.