Исследование печатной платы по неполной системе собственных функций.
При неполной системе собственных функций теоретически можно:
• определить координаты наиболее опасных мест установки микросхем;
• использовать такой критерий оценки качества платы, как несовпадение резонансных частот упругих систем конструкции;
• сформулировать рекомендации по изменению способов крепления с целью увеличения значений первых резонансных частот и, следовательно, уменьшения коэффициента усиления вибраций.
Проблема локализации наиболее опасных точек платы сводится к нахождению экстремумов функций двух независимых переменных – координатных функций. Экстремум находят по следующей схеме. Определяют первые частные производные координатной функции 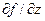 и
и 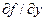 . Решают систему уравнений
. Решают систему уравнений 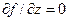 и
и 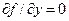 .
.
Полученные систему решений (z1,y1), (z2,y2) подставляют во вторые производные координатной функции: 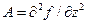 ;
; 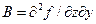 ;
; 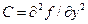 .
.
Затем составляют определитель: 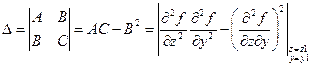
Если 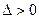 , то функция
, то функция 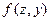 для системы значения (z1,y1) имеет максимум при
для системы значения (z1,y1) имеет максимум при 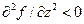 и минимум при
и минимум при 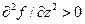 . Если
. Если 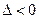 , то функция не имеет экстремумов.
, то функция не имеет экстремумов.
Например, точки экстремума функции 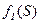 имеют координаты (
имеют координаты ( 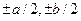 ).
).
Дата добавления: 2016-07-18; просмотров: 1801;











