Частоты и формы собственных колебаний печатной платы как тонкой пластины. Сопоставление способов ее крепления граничным условиям.
Формы главных колебаний платы как тонкой пластинки определяют исследуя уравнения ее свободных колебаний. Будем считать плату изотропной. Тогда уравнение ее свободных колебаний имеет следующий вид: 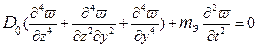 (1),
(1),
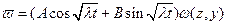 . Решение этого уравнения – формы и частоты собственных колебаний плат, которые должны удовлетворять конкретным краевым условиям. Например, для зажатого края граничные условия получают из условия равенства нулю прогиба и угла наклона касательной:
. Решение этого уравнения – формы и частоты собственных колебаний плат, которые должны удовлетворять конкретным краевым условиям. Например, для зажатого края граничные условия получают из условия равенства нулю прогиба и угла наклона касательной:
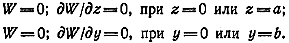
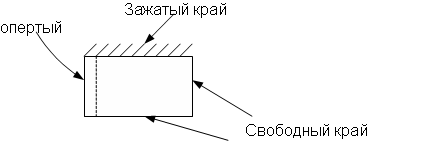
В теории пластин и оболочек исследованы платы, граничные условия для которых являются сочетанием зажатого, опертого и свободного краев. Эти способы крепления позволяют получить полную систему собственных функций и, следовательно, частотную характеристику. Поскольку область платы прямоугольна, формы главных колебаний определяют из ортогональной в прямоугольнике тригонометрической системы:
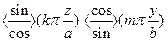
Тогда собственные функции: 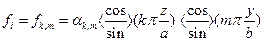 ,
,
где a,b – длины сторон платы, 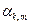 - коэффициент зависящий от способа крепления платы.
- коэффициент зависящий от способа крепления платы.
Откуда в общем случае 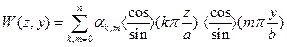 .
.
Собственные частоты в общем виде: 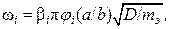
где 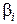 - постоянные коэффициенты,
- постоянные коэффициенты, 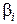 ,
, 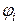 - зависят от способа крепления платы.
- зависят от способа крепления платы.
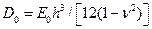 - жесткость изгиба платы, E0- модуль упругости,
- жесткость изгиба платы, E0- модуль упругости, 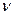 -коэффициент Пуассона материала платы.
-коэффициент Пуассона материала платы.
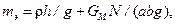 h – толщина платы; r – плотность материала платы;
h – толщина платы; r – плотность материала платы;
GM– вес микросхемы; N – количество микросхем платы.
Полная система собственных функций получена только для ограничен-ного количества сочетаний свободного, опертого и зажатого краев. Таким образом, получение частотной характеристики – сложная задача. Для различных сочетаний указанных граничных условий получена формула для первой собственной частоты: 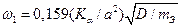 , где
, где 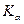 - коэффициент, зависящий от a,b и способов крепления сторон платы.
- коэффициент, зависящий от a,b и способов крепления сторон платы.
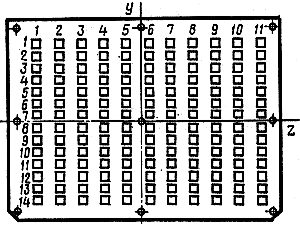
Способы крепления плат с точечным зажатием (крепление болтами/шпильками через втулки) не позволяют найти полную систему собственных функций и, следовательно, частотную характеристику расчетным путем. Для них можно определить только отдельные собственные формы fiи собственные значения li=wi2. Например, для платы
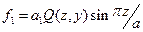
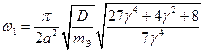
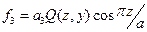
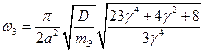
Дата добавления: 2016-07-18; просмотров: 3102;











