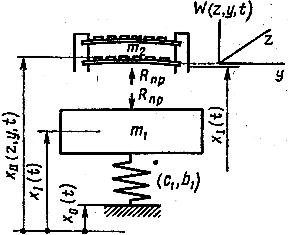
Расчетная модель конструкции с сосредоточенными и распределенными параметрами.
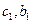 - жесткость и коэффициент демпфирования амортизаторов в главном геометрическом направлении;
- жесткость и коэффициент демпфирования амортизаторов в главном геометрическом направлении;
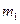 - масса корпуса ЭВМ и всех жесткосвязанных с ним элементов;
- масса корпуса ЭВМ и всех жесткосвязанных с ним элементов;
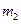 - суммарная масса плат.
- суммарная масса плат.
Разобьем модель на два участка: плата с опорным контуром – упругая система; твердое тело с нежесткой механической связью ( 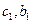 ) – одномассовая система. Рассмотрим отдельно эти участки. Движение платы будет совершаться под действием кинематической возмущения за счет движения ее опорного контура по закону
) – одномассовая система. Рассмотрим отдельно эти участки. Движение платы будет совершаться под действием кинематической возмущения за счет движения ее опорного контура по закону 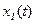 и силы
и силы 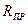 (приведенная реакция системы), а движение твердого тела – по закону
(приведенная реакция системы), а движение твердого тела – по закону 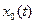 и силы
и силы 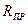 .
.
Представим относительное перемещение платы в виде ряда по формам ее главных колебаний: 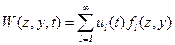 , тогда
, тогда 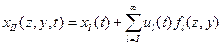 , где
, где 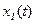 - переносное движение упругой системы как твердого тела вместе с ее опорным контуром;
- переносное движение упругой системы как твердого тела вместе с ее опорным контуром; 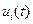 - перемещение точки упругой системы в i-м главном колебании относительно ее недеформированного состояния;
- перемещение точки упругой системы в i-м главном колебании относительно ее недеформированного состояния; 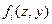 - форма i-го главного колебания упругого тела (нормальная функция).
- форма i-го главного колебания упругого тела (нормальная функция).
Основное положение – главное колебание упругого тела может совершаться независимо от других его колебаний. Следствие – движение системы в каждом главном направлении можно рассматривать отдельно. Для i-го главного колебания упругой системы:
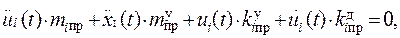 где
где
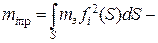 приведенная масса упругой системы в i-м главном колебании;
приведенная масса упругой системы в i-м главном колебании;
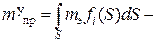 приведенная масса упругой системы при ее переносном движении по закону
приведенная масса упругой системы при ее переносном движении по закону 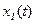 ;
;
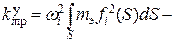 приведенный коэффициент жесткости;
приведенный коэффициент жесткости;
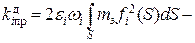 приведенный коэффициент демпфирования.
приведенный коэффициент демпфирования.
Здесь mэ– масса элементарной площадки упругого тела (платы); S = (z, y); wi– частота главного колебания; ei– логарифмический декремент затухания i-го главного колебания, деленный на 2p. Теперь уравнение движения упругой системы (пакета плат) в i-м главном колебании будет (а):
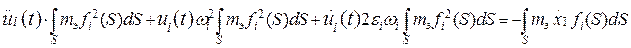 Реакция упругой системы (платы) на основание
Реакция упругой системы (платы) на основание 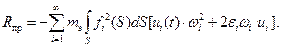
Тогда дифференциальное уравнение движения одномассовой системы будет (б):
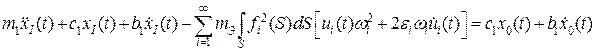 .
.
Решая систему (а) и (б) получаем частотную характеристику:
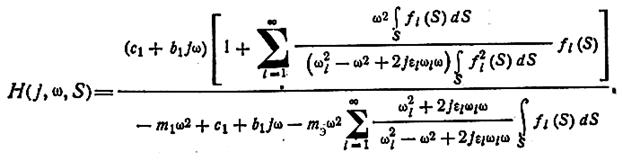
Дата добавления: 2016-07-18; просмотров: 1799;











