Плоская электромагнитная волна в диэлектрике. Скорость распространения электромагнитной волны
При исследовании процессов в переменном электромагнитном поле пользуются полной системой уравнений Максвелла.
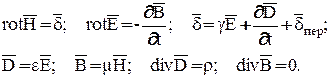
Здесь 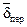 - плотность тока переноса
- плотность тока переноса
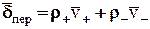 ,
,
где r+ и r- - объемная плотность положительно заряженных частиц и отрицательно заряженных частиц, перемещающихся в пространстве со скоростью 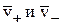 соответственно.
соответственно.
Для плоской, поляризованной электромагнитной волны, излучаемой источниками, не содержащими постоянных токов и зарядов (антенна), и распространяющейся в идеальном диэлектрике (g=0), уравнения электромагнитного поля можно преобразовать к следующему виду:
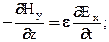 (4.1)
(4.1)
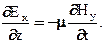 (4.2)
(4.2)
Отметим, что электромагнитная волна называется плоской, когда векторы 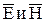 зависят только от одной координаты, например z.
зависят только от одной координаты, например z.
Поляризованной называется такая волна, в которой вектор напряженности электрического поля все время остается параллельным некоторому направлению (например, как в нашем случае, оси ох), а вектор напряженности магнитного поля – другому (оси оy).
Такие условия обеспечиваются при излучении электромагнитных волн неподвижной антенной на достаточно большом расстоянии от нее.
Таким образом, в электромагнитной волне, свободно распространяющейся в однородном и изотропном диэлектрике, векторы 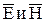 взаимно перпендикулярны (
взаимно перпендикулярны ( 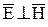 ).
).
Уравнения (4.1) и (4.2) можно преобразовать к следующему виду:
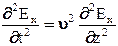 , (4.3)
, (4.3)
где 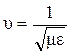 имеет размерность скорости.
имеет размерность скорости.
Уравнение (4.3) является уравнением колебаний или волновым уравнением и относится к гиперболическому типу.
Как известно, решение такого уравнения всегда можно представить в виде:
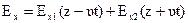 . (4.4)
. (4.4)
При этом составляющая Ех1 называется прямо бегущей или прямой волной (перемещается в положительную сторону оси oz со скоростью u), а составляющая Ех2 – обратно бегущей или обратной волной (перемещается в отрицательную сторону оси oz со скоростью u).
Используя выражения (4.1), (4.2) и (4.4) получаем формулу для напряженности магнитного поля
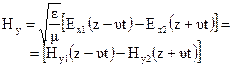
Составляющие Нх1 и Нх2 также называют прямой и обратной волной.
Таким образом, электромагнитная волна распространяется в пространстве со скоростью u (в прямом или в обратном направлении).
В частности, в пустоте (m=m0, e=e0) эта скорость равна скорости света (u=2.998×108м/с»3×108м/с).
Если существует только прямая или только обратная волна, то энергии электрического и магнитного полей равны между собой, так как при этом равны их объемные плотности
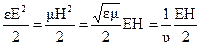 .
.
Отношение Ех1/Ну1=Ö`m¤e=Zв имеет размерность электрического сопротивления и называется волновым сопротивлением среды.
В частности, для пустоты Zв=377Ом (Zв =120p).
Таким образом, для любой среды
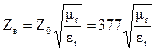 .
.
В случае, если прямая электромагнитная волна распространяется в среде, абсолютное значение магнитной проницаемости которой m=m1, а абсолютное значение диэлектрической проницаемости e=e1, и подходит нормально (перпендикулярно) к плоской границе, разделяющей данную среду и среду с m=m2 и e=e2, то прямая волна (Ех1=Еj1, Нх1=Нj1) частично будет проходить сквозь поверхность раздела, образуя во второй среде преломленную (прямую) волну (Еj2, Нj2), а частично будет отражаться от поверхности раздела, образуя в первой среде отраженную (обратную) волну (Ех2=Еy1, Нх2=Нy1).
Соотношение между напряженностями поля для этих волн на поверхности раздела можно представить следующим образом:
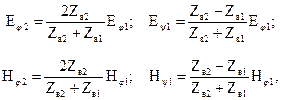
где 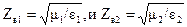 -соответствующие волновые сопротивления первой и второй среды.
-соответствующие волновые сопротивления первой и второй среды.
Если волновые сопротивления сред равны между собой (Zв1= Zв2), то отраженные волны отсутствуют.
В случае, когда источник (антенна) излучает электромагнитную волну, в которой напряженность электрического и магнитного поля изменяется по гармоническому закону, то для прямой волны
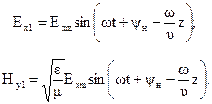
Здесь yн- начальная фаза; w - угловая частота колебаний (w=2pf).
Расстояние, на которое распространяется электромагнитная волна в течение одного периода колебаний Т (Т=1/f), называется длиной волны
l = uТ = u/f.
Из данного выражения видно, что длина волны в диэлектрике обратно пропорциональна частоте f. Так, при частоте f=1 МГц длина волны в пустоте равна 300 м, а при f=50Гц l=6000 км.
Вектор Пойнтинга
Для анализа электромагнитных полей, широко используют вектор Пойнтинга 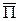 . Этот вектор имеет размерность мощности (энергии в единицу времени), передаваемой сквозь единицу поверхности, нормальной к направлению распространения волны, и определяется следующим соотношением:
. Этот вектор имеет размерность мощности (энергии в единицу времени), передаваемой сквозь единицу поверхности, нормальной к направлению распространения волны, и определяется следующим соотношением:
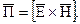 (4.5)
(4.5)
В теории электромагнитного поля довольно большое значение имеет теорема Умова-Пойнтинга, которая описывает энергетические соотношения в поле
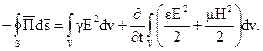 (4.6)
(4.6)
Левая часть данного выражения представляет поток вектора Пойнтинга (направленный внутрь объема V) сквозь любую замкнутую поверхность S, ограничивающую некоторый объем V. Часто уравнение (4.6) записывают и в таком виде
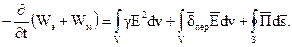 (4.7)
(4.7)
Здесь WЭ и WМ – энергия соответственно электрического и магнитного поля, заключенных в объеме V.
В более общем случае, внутри объема V могут существовать источники электромагнитной энергии, в которых совершается преобразование энергии какого-либо вида или механической работы в электромагнитную энергию. Обозначив через ре мощность этих источников, получим
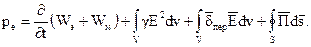 (4.8)
(4.8)
Дата добавления: 2016-07-18; просмотров: 3116;











