Расчет индуктивностей

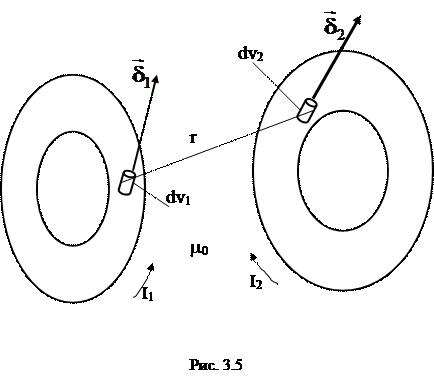
Общее выражение для взаимной индуктивности двух контуров произвольной формы (рис. 3.5), выполненных из немагнитного материала и расположенных в воздухе, выглядит следующим образом:

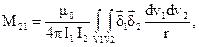
где V₁ и V₂ – объемы пространства, занимаемого первым и вторым контуром; r – расстояние от элемента объема dv₁ первого контура до элемента объема dv₂ второго контура; 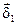- вектор плотности тока в точках элемента объема dv₁; 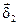- вектор плотности тока в точках элемента объема dv₂.

Как было отмечено выше, при m = const взаимная индуктивность не зависит от токов в контурах. Наличие токов в последнем выражении не противоречит этому положению, поскольку при постоянных токах их можно внести под знаки интегралов, и тогда в подынтегральном выражении получим отношение плотности тока к соответствующему току, которое определяется только формой проводника.

Общее выражение для собственной индуктивности контура можно получить, пользуясь общим выражением для взаимной индуктивности двух контуров. Для этого необходимо представить два совершенно одинаковых контура, сближающихся до полного слияния так, что один из них занимает объем другого. После такого слияния, по существу, уже остается только один контур. Из выражения для М₂₁ нетрудно получить выражение для L такого контура, положив I₁ = I₂ = I и V₁ = V₂ = V. Имеем

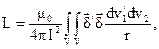
причем 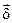- плотность тока в элементе dv; 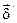- плотность тока в элементе dv^/ одного и того же проводника; r – расстояние между этими элементами объема. Интегрирование производится дважды по всему объему проводника V.

Формулы для индуктивности весьма упрощаются для контуров из линейных проводников, поперечные размеры сечений которых весьма малы. При вычислении собственной индуктивности таких проводников ее подразделяют на внутреннюю (L_ВТ) и внешнюю (L_ВШ) и общую индуктивность определяют путем их суммирования.

Ниже приведены выражения для индуктивностей простейших систем.

Индуктивность тонкого цилиндрического проводника длиной l и радиусом R (длина много больше радиуса)

.

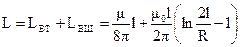Индуктивность отрезка цилиндрического проводника длиной l и радиусом R

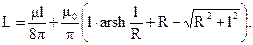
Индуктивность двухпроводной линии на длине l

.

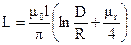Здесь D – расстояние между проводами; R – радиус проводов (R << D).

Индуктивность параллельных цилиндров длиной l, с радиусами R₁ и R₂ и расстоянием между осями D

.

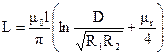Индуктивность круглого кольца радиусом r из тонкого цилиндрического провода диаметром d

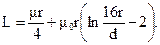
Если провод выполнен из неферромагнитного материала, то

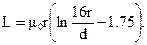
Индуктивность прямоугольной рамки из тонкого круглого провода

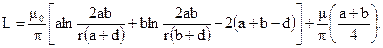
Здесь а и b – длины сторон рамки; d – диагональ рамки; r – радиус провода (r << а; r << b).