Примеры расчета магнитного поля
Пример 1. По длинному полому биметаллическому проводу, расположенному в воздухе, протекает постоянный ток I = 200 А (рис. 3.6). Радиус отверстия, внутреннего и наружного провода равны соответственно r0 = 4 мм, r1 = 8 мм и r2 = 16 мм. Внутренний провод выполнен из меди (g1 = 58 мкСм/м), наружный из алюминия (g2 = 34 мкСм/м).
Определить закон изменения векторного потенциала и магнитной индукции внутри и вне провода. Построить графики изменения этих величин вдоль радиуса. Найти индуктивность провода на единицу длины.
Решение. Поскольку поле в данном случае обладает цилиндрической симметрией, то данную задачу можно решить с помощью закона полного тока, представленного в интегральной форме (3.3). Для этого разобьем область исследования на четыре подобласти. В первой подобласти (0 £ r £ r0) напряженность магнитного поля равна нулю. Для определения напряженности поля во второй подобласти (r0 £ r £ r1), проводим окружность произвольным радиусом r с центром на оси провода и для контура, образованного данной окружностью применяем закон полного тока. С учетом того, что вектор напряженности направлен по касательной к окружности и по величине остается неизменным, выражение (3.3) можно представить в следующем виде:
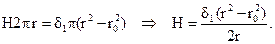
Аналогично определяется напряженность поля в третьей подобласти (r1 £ r £ r2)
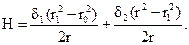
Таким образом, для определения напряженности поля в соответствующих подобластях необходимо рассчитать плотность тока d1 и d2
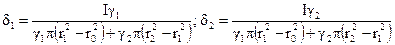 .
.
После подстановки в последние выражения соответствующих величин получаем d1 = 396.5 кА/м2, d2 = 232.4 кА/м2.
Напряженность поля в четвертой подобласти (r2 £ r £ ¥) определяется с помощь следующего выражения:
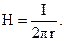
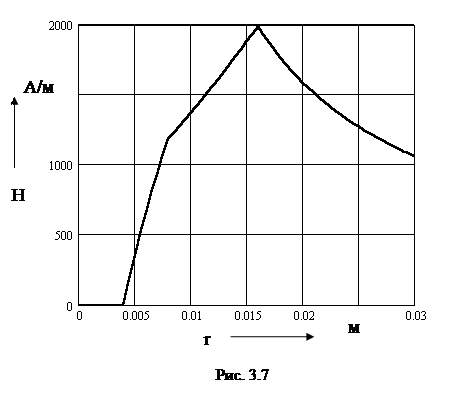 |
Изменение напряженности вдоль радиуса показано на рис. 3.7.
Отметим, что поскольку магнитная проницаемость во всей области одна и та же, то распределение магнитной индукции вдоль радиуса полностью повторяет распределение напряженности поля.
Для нахождения векторного потенциала необходимо для каждой из подобластей записать уравнение Пуассона (3.7) или Лапласа (3.8) и провести их совместное решение. Эти уравнения удобнее записывать в цилиндрической системе координат. При этом необходимо учитывать, что в данной задаче векторный потенциал имеет только одну составляющую, направленную по оси провода (по оси z) и эта составляющая зависит только от радиуса r. Раскрывая лапласиан в указанной системе координат, будем иметь:
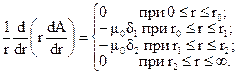
Интегрируя дважды по r, получаем выражения для потенциала для каждой подобласти:
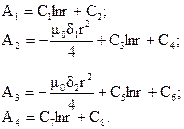
Слагаемое С1lnr должно отсутствовать, так как А не может принимать бесконечно больших значений при r = 0. Отсюда следует, что постоянная интегрирования С1 = 0. Векторный потенциал определяется с точностью до постоянной. Примем эту постоянную равной нулю: С8 = 0. Для определения оставшихся шести постоянных составим с помощью граничных условий систему уравнений. Эти граничные условия определяют равенство на границе раздела двух сред касательных составляющих напряженности поля и равенство векторного потенциала.
Касательной в данной задаче является угловая составляющая напряженности поля, которая определяется с помощью выражения (3.6) следующим образом:
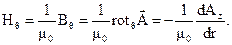
Таким образом, для определения постоянных интегрирования получаем систему уравнений:
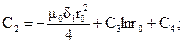
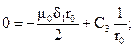
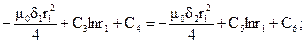
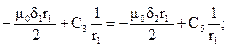
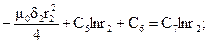
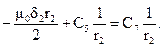
Решая совместно данные уравнения, получаем: С2 = 1.845×10-4; С3 = 3.986×10-4;
С4 =2.085×10-4; С5 = -2.612×10-6; С6 = 1.733×10-4; С7 = -4×10-4.
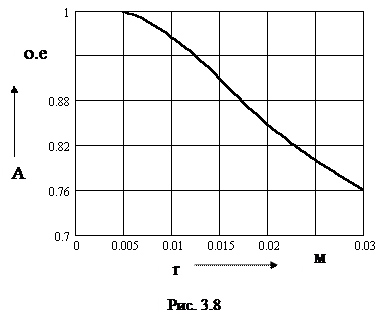 |
На рис. 3.8 показано распределение векторного потенциала вдоль радиуса. Данные на графике представлены в относительных единицах. За базисное значение принято значение потенциала в первой зоне А1 = 1.845×10-4 Вб/м.
Для определения индуктивности провода вначале найдем магнитный поток, пронизывающий биметаллический провод на длине, равной одному метру.
Для этого воспользуемся формулой (3.10), которую, с учетом того, что векторный потенциал направлен вдоль оси провода, а в подынтегральном выражении стоит скалярное произведение двух векторов, можно преобразовать к следующему виду:
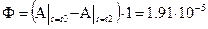 Вб.
Вб.
Таким образом, индуктивность (на один метр длины) биметаллического провода равна: L = Ф/I = 95.5×10-9 Гн/м.
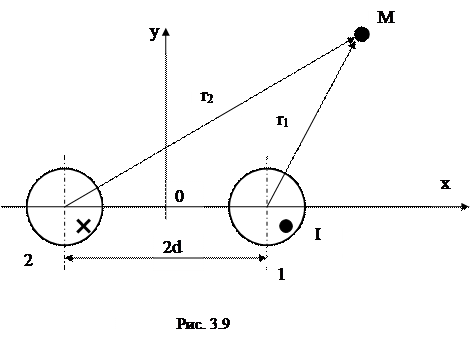
Пример 2. Рассчитать напряженность магнитного поля двухпроводной линии с током I = 2700 А, провода которой выполнены из алюминия и имеют радиус R = 28 мм. Расстояние между проводами 2d = 20 м (рис. 3.9).
Решение. Решение данной задачи можно получить либо с помощью закона полного тока, либо с использованием функции векторного магнитного потенциала. Выражение векторного потенциала внутри цилиндрического провода с током и вне его, уже получено в предыдущем примере. Так, внутри провода (0 £ r £ R) оно имеет вид:
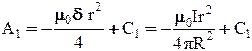 ,
,
а вне провода (R £ r £¥) –
 |
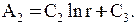
Постоянные интегрирования определяются из условий равенства на поверхности провода векторного потенциала (А1 = А2, при r = R) и его нормальных производных (dА1/dr = dА2/dr, при r = R)
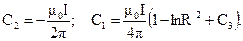
Нас интересует поле только вне провода, поэтому выражение для потенциала в этой области с точностью до постоянной будет иметь вид:
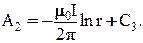
Используя данную формулу, запишем выражение для определения векторного потенциала в произвольной точке М (рис. 3.9) от двух проводов
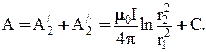
Примем значение постоянной С равной нулю (это означает, что за точку нулевого потенциала мы приняли начало координат) и перепишем последнее выражение в прямоугольной системе координат
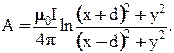
С помощью выражения (3.6) найдем составляющие напряженности магнитного поля
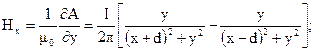
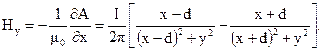
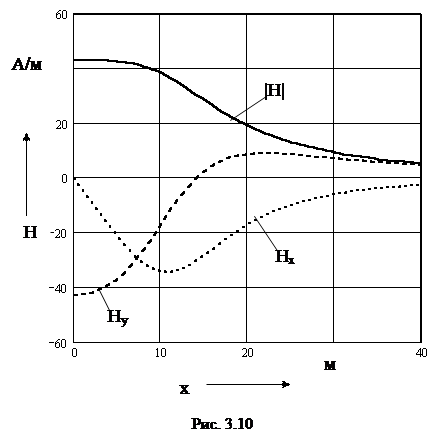
при у = 10 м показано на рис. 3.10.
Распределение данных составляющих, а также модуля напряженности магнитного поля, который определяется по формуле
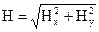 ,
,
Дата добавления: 2016-07-18; просмотров: 3432;











