Механические силы в магнитном поле

Пусть существует система из n магнитносвязанных электрических цепей, в которых протекают постоянные токи. Пусть одна из цепей перемещается в на­правлении оси х на величину dx. При перемещении цепи будет выполнена ме­ханическая работа:

,

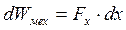где F_x - сила, действующая на цепь в направлении х.

Вследствие перемещения цепи произойдет изменение магнитного поля системы:

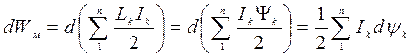
Изменение потокосцепления каждой цепи Ψ_k вызовет появление напря­жения на ее зажимах: 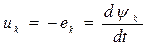, при этом в системе будет выполнена до­полнительная электрическая работа:

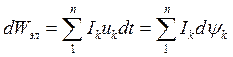
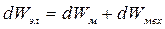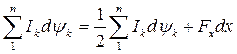В соответствии с законом сохранения энергии составим баланс энергий: , или , откуда следует, что

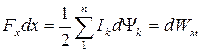, или 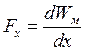, т. е. составляющая силы, действую­щей на электрическую цепь в произвольном направлении равна производной от энер­гии магнитного поля в этом же направлении.

Составляющие силы, действующей на электрическую цепь в направ­лении осей координат x, y, z:

.

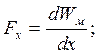
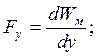
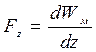Результирующая сила:

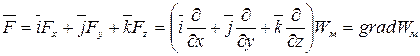
Результирующая сила направлена в сторону наибольшего возрастания энергии магнитного поля.

Так как по условию токи цепей постоянны, то и энергия собственного магнитного поля, равная 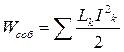тоже постоянна, а изменяется только взаимная энергия системы W_вз и, следовательно, сила .

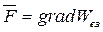Если система состоит только из двух магнитносвязанных цепей, то энер­гия магнитного поля будет равна:

.

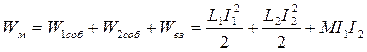Тогда получим:

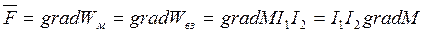
В измерительных приборах электродинамической системы вращающий момент, действующий на подвижную систему прибора, будет равен:

,

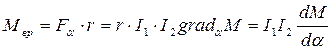т.е. вращающий момент пропорционален скорости изменения взаимной индук­тивности М при повороте подвижной системы прибора.