Уравнения магнитного поля в интегральной и дифференциальной формах

Магнитное поле характеризуется двумя векторными величинами:

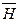– вектор напряженности магнитного поля, создается электрическими токами, явля­ется первопричиной магнитного поля [А/м];

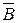– вектор индукции магнитного поля или плотность магнитных силовых линий [Тл].

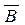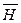Между векторами и существует связь:

,

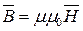где m₀ = 4×p×10^-7 » 1,257× 10^-6 [Гн/м] - магнитная проницаемость пустоты, m - относитель­ная магнитная проницаемость.

Известный из курса физики закон Био-Савара-Лапласа устанавливает связь между элементар­ным вектором магнитной индукции 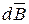в произвольной точке про­странства и элементом тока 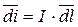(рис. 274):

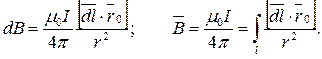
На основе закона Био-Савара-Лапласа выполняется расчет магнитного поля слож­ных систем проводников с токами.

Закон Ампера определяет силу взаимодействия магнитного поля на эле­мент провод­ника с током:

^,

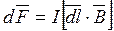откуда следует, что сила, действующая на проводник , равна

^.

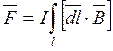На прямолинейный проводник с током I в равномерном магнитном поле действует сила 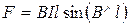, направление которой определяется по правилу левой руки.

1 –й закон Кирхгофа для магнитной цепи, выражающий непрерывность магнитных силовых линий поля, имеет вид:

- интегральная форма уравнения непре- рывности магнитных линий.

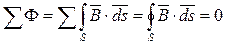
Преобразуем это уравнение по теореме Остроградского-Гаусса:

- дифференциальная форма уравнения непрерывности магнитных линий.

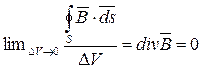
Закон полного тока для магнитного поля имеет вид:

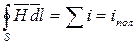- интегральная форма закона полного тока. Преобразуем левую часть этого уравнения по теореме Стокса: 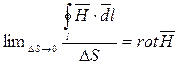, а в пра­вой части получим: 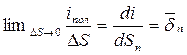. Следовательно:

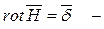дифференциальная форма закона полного тока.

Граничные условия в магнитном поле на границе раздела двух сред с раз­личными магнитными проницаемостями m₁ и m₂ выражаются уравнениями:

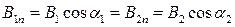
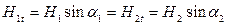
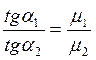
На границе раздела двух сред равны нормальные составляющие вектора В и танген­циальные составляющие вектора Н.

Магнитное поле несет в себе энергию, плотность которой определя­ется уравне­нием:

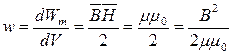[ Дж/м³]