Векторный потенциал магнитного поля
Пусть требуется рассчитать магнитное поле в однородной среде (m=const) , в которой протекает электрический ток, плотность которого задана в виде некоторой функции координат 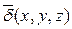 . Для определения векторов поля
. Для определения векторов поля 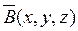 и
и 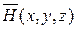 необходимо решить систему уравнений:
необходимо решить систему уравнений:
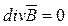 (1)
(1)
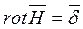 (2)
(2)
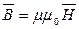 (3)
(3)
Введем новую векторную величину 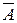 , позволяющую исключить из системы уравнений неизвестные
, позволяющую исключить из системы уравнений неизвестные 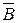 и
и 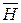 и получить одно дифференциальное уравнение, решение которого известно в математике.
и получить одно дифференциальное уравнение, решение которого известно в математике.
Пусть вектор 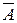 , получивший название вектора потенциала магнитного поля, удовлетворяет условию:
, получивший название вектора потенциала магнитного поля, удовлетворяет условию: 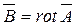
Так как divrot любого вектора тождественно равна нулю, то уравнение (1) выполняется тождественно: 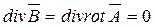
Из уравнения (2) следует: 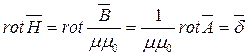
Из курса математики известно, что 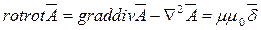 .
.
В полученном уравнении можно принять 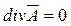 , не нарушая равенства
, не нарушая равенства 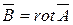 . Тогда получим :
. Тогда получим :
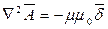 - уравнение Пуассона для векторного потенциала магнитного поля для областей среды, где протекают токи проводимости. Для областей среды, где токи проводимости отсутствуют, уравнение Пуассона превращается в уравнение Лапласа
- уравнение Пуассона для векторного потенциала магнитного поля для областей среды, где протекают токи проводимости. Для областей среды, где токи проводимости отсутствуют, уравнение Пуассона превращается в уравнение Лапласа 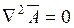 . Каждое из этих векторных уравнений в декартовой системе координат распадается на три скалярных в направлении координатных осей:
. Каждое из этих векторных уравнений в декартовой системе координат распадается на три скалярных в направлении координатных осей:
 |  |
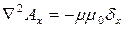
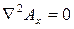
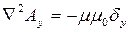
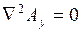
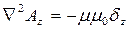
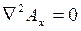
Решения уравнений Пуассона для векторного потенциала 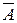 имеют вид (без вывода):
имеют вид (без вывода):
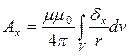 ;
; 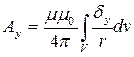 ;
; 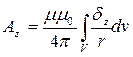
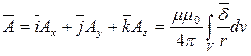
Если решение для векторного потенциала 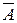 найдено, то другие неизвестные величины выражаются через векторный потенциал:
найдено, то другие неизвестные величины выражаются через векторный потенциал:
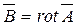
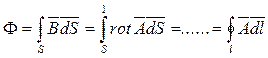
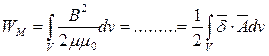
Если токи протекают по линейным проводникам, поперечные размеры которых весьма малы по сравнению с их длиной, то то выражение для векторного потенциала 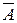 можно упростить следующим образом:
можно упростить следующим образом:
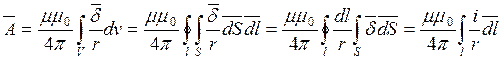
где 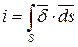 - ток в проводнике
- ток в проводнике
В последнем уравнении интегрирование по объему заменяется интегрированием по контурам линейных проводов, что упрощает его решение.
Дата добавления: 2020-07-18; просмотров: 662;











