Методы расчета электрических полей постоянного тока

Электрическое поле постоянного тока, с одной стороны, и электростати­ческое поле вне электрических зарядов (r_св=0), с другой стороны, описываются одинаковыми по струк­туре математическими уравнениями. Для сравнения све­дем эти уравнения в общую таб­лицу.

Электрическое поле постоянного тока	Электростатическое поле при отсут­ствии зарядов (rсв=0)

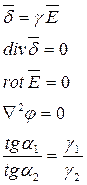
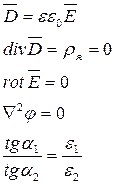
Как следует из приведенной таблицы оба поля описываются одинаковыми по струк­туре уравнениями и к ним применим принцип двойственности. Таким образом для расчета электрических полей постоянного тока можно применять те же расчетные методы, которые были получены ранее для электростатических полей, при условии соответствующих замен в расчетных формулах физических величин и коэффициентов: 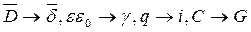. С другой стороны, для экспериментального исследования сложных по конфигурации электроста­тических полей применяется их физическое модели­рование с помощью элек­трических полей постоянного тока.

В электростатике очень важное значение имеет теоретическое понятие точечного за­ряда q. По аналогии введем понятие точечного тока i, который рас­текается в проводящей среде из одной точки, при этом в этой точке плотность тока .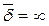

Рассмотрим несколько примеров расчета электрических полей постоян­ного тока.

Пример 1. Заземлитель шаровой формы с радиусом R находится на боль­шой глубине h (h>>R). К заземлителю подведено напряжение U (рис. 270).

Заменим суммарный ток, стекающий с поверхности заземлителя точеч­ным током i, который растекается из центра заземлителя. Применим расчетные формулы из теории элек­тростатического поля точечного заряда, заме­нив :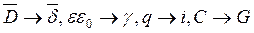

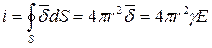, откуда 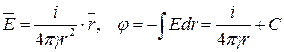, если принять 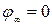, то постоянная интегрирования С=0.

Потенциал на поверхности заземлителя при r = R:

,

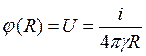откуда получаем формулы для сопротивления заземлителя и его тока:

.

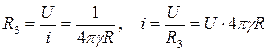Пример 2. Заземлитель в виде шара расположен на сравнительно не­большой глу­бине h, соизмеримой с его радиусом R (рис. 271).

Применим к решению задачи метод зеркальных отображений. Заменим в верхней полуплоскости диэлектрик 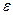проводящей средой γ и зеркально распо­ложим там такой же заземлитель той же полярности, при этом граничные усло­вия на поверхности земли не из­менятся (линии вектора Е направлены по каса­тельной вдоль поверхности). Заменим токи, стекающие с поверхностей обоих заземлителей, равными по величине точечными токами, растекающимися из электрических центров 1 и 2, которые будут смещены относительно геометри­ческих центров так, чтобы сохранились прежними граничные условия на по­верх­ности шаров (поверхности должны остаться эквипотенциальными с потен­циалом φ=U). После определения положения электрических центров расчет па­раметров поля в произ­вольной точке n производится по методу наложения:

.

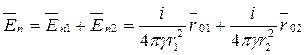
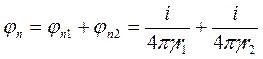При соотношении h>>R потенциал на поверхности заземлителя будет ра­вен:

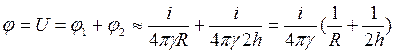, откуда следует формула для определения сопротивления заземлителя:

.

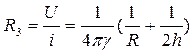Пример 3. Определить шаговое напряжение 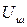на заданном расстоянии х от центра опоры высоковольтной ЛЭП при коротком замыкании одной из фаз линии на опору (рис. 272).

Для упрощения расчетов будем считать, что заземлитель опоры имеет форму полу­шария с радиусом R. Заменим диэлектрик в верхней части про­странства проводящей средой γ, а заземлитель дополним зеркальным отображе­нием до полного шара. После таких преоб­разований решение задачи сводится к расчету поля шарового заземлителя п.1.:

,

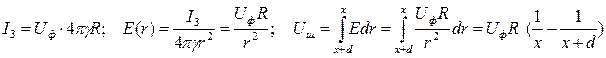где 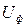- фазное напряжение ЛЭП, R – радиус заземлителя опоры.

Пример 4. Требуется рассчитать электрическое поле вертикального ци­линдриче­ского заземлителя диаметром D и длиной h. К заземлителю подведено напряжение U (рис. 273).

Заменим диэлектрик в верхней части пространства проводящей средой γ, а заземли­тель дополним его зеркальным отображением. Будем считать, что электрический ток сте­кает с оси заземлителя, где 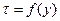- линейная плотность тока стекания [А/м]. Вид функ­ции 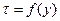должен удовлетворять граничным условиям, а именно, поверхность заземли­теля должна быть эквипотенциальной с потенциалом φ=U. Расчеты показывают, что ли­нейная плотность тока τ по концам заземлителя значительно больше, чем в его середине. Тогда di=tdl - элемент тока.

Параметры поля получаются в результате интегрирования соответствую­щих уравне­ний по всей длине заземлителя:

.

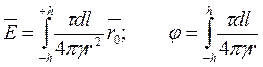Расчеты полей сложной конфигурации выполняются как правило на ЭВМ методом численного интегрирования соответствующих дифференциаль­ных уравнений.

T3. Магнитное поле постоянных токов