Законы электрического поля в интегральной и дифференциальной формах
Под электрическим током проводимости i понимается движение свободных зарядов в проводящей среде γ под действием сил электрического поля 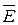 . Ток проводимости в каждой точке среды характеризуется вектором плотности:
. Ток проводимости в каждой точке среды характеризуется вектором плотности:
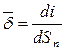 [А/м2].
[А/м2].
Направление вектора 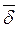 совпадает с направлением положительных зарядов. Ток, протекающий через произвольную площадку s, связан с вектором
совпадает с направлением положительных зарядов. Ток, протекающий через произвольную площадку s, связан с вектором 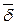 уравнением:
уравнением: 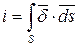 .
.
Выделим мысленно в проводящей среде, где протекает ток, элементарный цилиндр длиной dl с основанием ds так, чтобы вектор 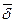 был направлен вдоль оси цилиндра (рис. 268).
был направлен вдоль оси цилиндра (рис. 268).

Ток, протекающий вдоль цилиндра:
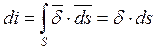 .
.
Напряжение между концами цилиндра:
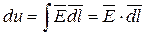 ,
,
где 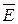 - вектор напряженности электрического поля, под действием которого возникает ток.
- вектор напряженности электрического поля, под действием которого возникает ток.
Сопротивление цилиндра, как проводника:
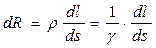 ,
,
где γ – удельная проводимость среды [См/м].
Сопротивление цилиндра по закону Ома:
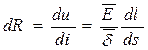 .
.
Приравнивая правые части равенств, получим:
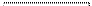 | |||
| |||
Мощность, выделяемая в цилиндре по закону Джоуля:
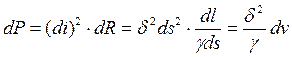 , откуда
, откуда
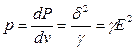 [Вт/м3] - уравнение закона Джоуля в дифференциальной форме, которое характеризует интенсивность выделения энергии вокруг рассматриваемой точки.
[Вт/м3] - уравнение закона Джоуля в дифференциальной форме, которое характеризует интенсивность выделения энергии вокруг рассматриваемой точки.
Если внутри цилиндра окажутся источники энергии, создающие дополнительную составляющую напряженности поля 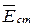 (напряженность поля сторонних сил), то
(напряженность поля сторонних сил), то 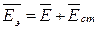 и закон Ома в дифференциальной форме получит вид:
и закон Ома в дифференциальной форме получит вид:
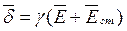 .
.
Как известно, выражение первого закона Кирхгофа в интегральной форме имеет вид:
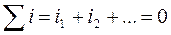 .
.
Выразим каждый из токов 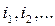 через вектор плотности тока
через вектор плотности тока 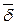 :
:
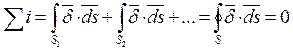 .
.
Преобразуем полученное уравнение по теореме Остроградского-Гаусса:
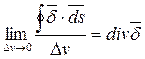 , следовательно:
, следовательно:
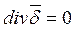 - уравнение первого закона Кирхгофа в дифференциальной форме.
- уравнение первого закона Кирхгофа в дифференциальной форме.
Из этого уравнения следует вывод, что линии вектора 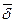 непрерывны и замкнуты.
непрерывны и замкнуты.
Интегральная форма уравнения 2-го закона Кирхгофа для контура, не содержащего источников ЭДС, имеет вид:
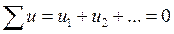 .
.
Выразим каждое из напряжений через вектор напряженности поля 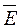 :
: 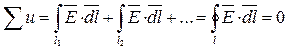 , и преобразуем полученное уравнение по теореме Стокса:
, и преобразуем полученное уравнение по теореме Стокса: 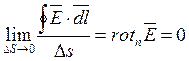 .
.
Последнее уравнение справедливо для любого направления, следовательно:
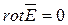 - уравнение второго закона Кирхгофа в дифференциальной форме.
- уравнение второго закона Кирхгофа в дифференциальной форме.
Из этого уравнения следует вывод, что электрическое поле постоянного тока безвихревое, потенциальное и в каждой точке может быть описано потенциальной функцией согласно уравнению:
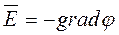 .
.
Преобразуем уравнение первого закона Кирхгофа:
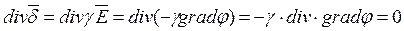 , откуда следует:
, откуда следует: 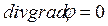 или
или 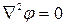 - уравнение Лапласа для электрического поля постоянного тока.
- уравнение Лапласа для электрического поля постоянного тока.
На границе раздела двух сред с различными проводимостями 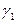 и
и 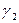 выделим точку и окружим ее элементарной призмой, у которой высота бесконечно мала по сравнению с линейными размерами оснований (рис. 269а).
выделим точку и окружим ее элементарной призмой, у которой высота бесконечно мала по сравнению с линейными размерами оснований (рис. 269а).

Применяя первый закон Кирхгофа, получим:
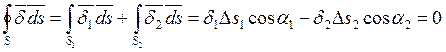 .
.
Откуда следует, что 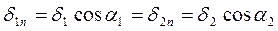 - на границе раздела двух сред с различными проводимостями равны нормальные составляющие вектора плотности тока
- на границе раздела двух сред с различными проводимостями равны нормальные составляющие вектора плотности тока 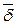 .
.
Окружим точку элементарным прямоугольником (рис. 269б), у которого высота бесконечно мала по сравнению с длиной. Применяя второй закон Кирхгофа к контуру прямоугольника, получим:
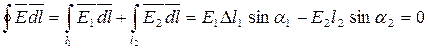 .
.
Откуда следует, что 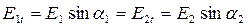 - на границе раздела двух сред с различными проводимостями
- на границе раздела двух сред с различными проводимостями 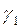 и
и 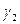 равны тангенциальные составляющие вектора напряженности поля
равны тангенциальные составляющие вектора напряженности поля 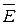 .
.
Разделим почленно левые и правые части полученных уравнений и учтем, что 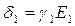 и
и 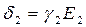 , в итоге получим:
, в итоге получим:
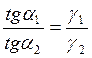
- условие преломления линий поля на границе раздела двух сред с различными проводимостями 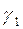 и
и 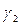 .
.
Дата добавления: 2020-07-18; просмотров: 748;











