Логарифмическое уравнение регрессии

В общем случае уравнение логарифмической функции имеет вид y = a Ln(x) + b.

Применение логарифмической функции в качестве уравнения регрессии возможно только в том случае, если в спектре значений аргумента X (диапазон ячеек A7:А18) отсутствуют нулевые и отрицательные значения.

Пусть исходная функция y = f(x) варианта задания имеет вид, показанный в таблице в диапазоне ячеек A7:B18, рис. 4.5.1.

Построим точечный график функции Логарифмическая регрессия y = f(x).

В строке 21 создадим шапку таблицы, как показано на рис. 4.5.1.

В ячейку B26 запишем произвольную константу 1, а в ячейку C26 - произвольную константу 2.

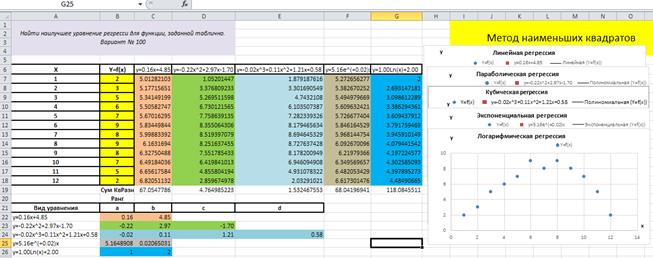
Рис. 4.5.1

В ячейку A26 запишем оператор присваивания для сцепленных символьных констант:

="y="&ТЕКСТ(B26;"0.00")&"Ln(x)"&ЕСЛИ(C26<0;ТЕКСТ(C26;"0.00");"+"&ТЕКСТ(C26;"0.00"))

Ячейке G6 присвоим такое же значение, какое приобретает ячейка A26, то есть G6 = A26.

Тогда, в соответствии с выбранными коэффициентами в ячейках B26=1 и C26=2, в ячейках A26 и G6получим результат y=1.00Ln(x)+2.00.

Запишем в ячейку G7 уравнение логарифмической функции с коэффициентами, взятыми в абсолютной адресации из ячеек B26 и C26, то есть =$B$26*LN(A7)+$C$26, в качестве аргумента X берётся значение ячейки A7исходной таблицы.

Скопируем закон преобразования информации ячейки G7 до ячейки G18 включительно.

В результате получим спектр значений функции y=1.00Ln(x)+2.00 на спектре аргументов X в диапазоне значений ячеек A7:A18, рис. 4.5.1.

В ячейку G19, используя мастер функций f_x, запишем результат вычисления функции =СУММКВРАЗН(B7:B18;G7:G18), рис. 4.5.2.

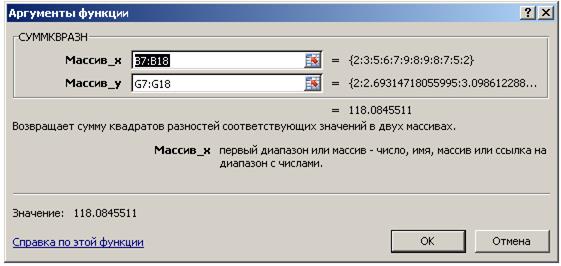
Рис. 4.5.2

Примечание: обозначение Массив_x и Массив_y, рис. 4.5.2, математическое и не совпадает с обозначениями выполняемого задания.

Добавим на точечный рисунок исходной таблицы уравнение логарифмической функции y=1.00Ln(x)+2.00, рис. 4.5.3.

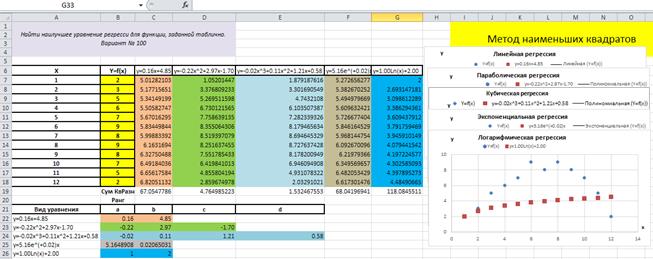
Рис. 4.5.3

Заметим, что это уравнение логарифмической регрессии, с произвольными значениями коэффициентов a=1 и b=2.

Соответствие этого уравнения регрессии исходному распределению оценено с помощью вычисления функции суммы квадратов разностей, значение которой составляет 118.0845511.

Для определения оптимальных значений коэффициентов a и b воспользуемся функцией Поиск решения:

– установим курсор в ячейку G19;

– последовательно, выбирая Разработчик, Данные, Поиск решения, вызвать окно Параметры поиска решения, в котором установить параметры, как показано на рис. 4.5.4, и нажать кнопку Найти решение;

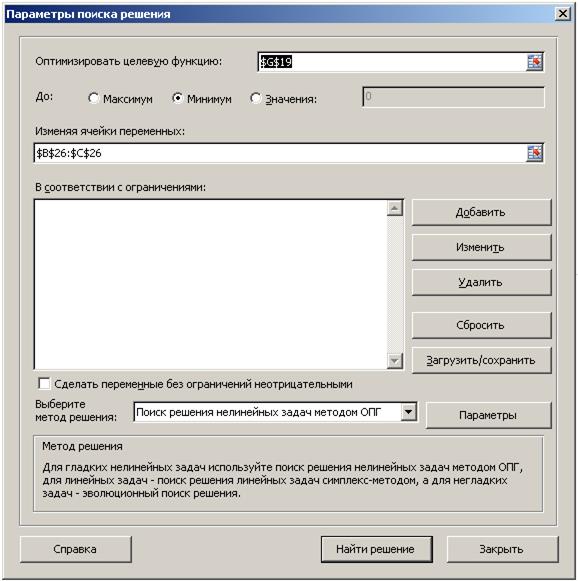
Рис. 4.5.4

– увидеть, как в ячейке B26 установится значение 1.59, в ячейке C26 – 3.28, в ячейке G19 – 55.12464582, рис. 4.5.5;

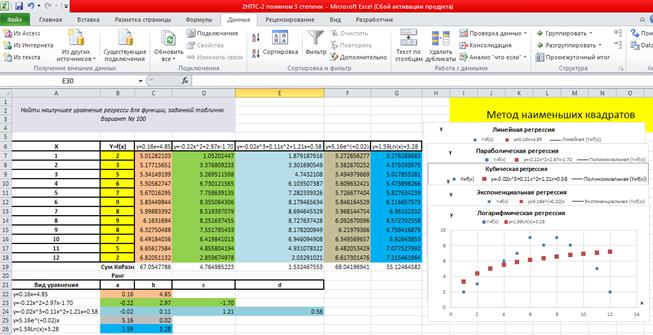
Рис. 4.5.5

Это означает, что логарифмическая функция с коэффициентами a = 1.59 и b = 3.28 отобразится на графике Логарифмическая регрессия, как показано на рис. 4.5.5, при этом значение суммы квадратов разностей будет минимально и равно 55.12464582.

Таким образом, коэффициенты для логарифмического уравнения регрессии определены и для исходного задания уравнение имеет вид y = 1.59Ln(x) + 3.28.

Чтобы убедиться в правильности решения щёлкнем правой клавишей мышки по любой точке исходного задания на графике Логарифмическая регрессия, рис. 4.5.5.

В появившемся окне выберем раздел Добавить линию тренда, рис. 4.5.6.

Рис. 4.5.6

В появившемся окне Формат линии тренда выбрать параметры Логарифмическая, показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2) и нажать кнопку Закрыть, рис. 4.5.7.

Рис. 4.5.7

Появившаяся на графике Логарифмическая регрессия линия тренда полностью совпадает с графиком построенного уравнения регрессии y = 1.59Ln(x) + 3.28, как и уравнение линии тренда y = 1.5852Ln(x) + 3.2763, что является доказательством правильности решения, рис. 4.5.8.

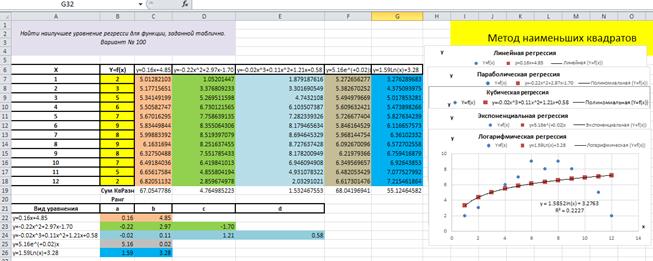
Рис. 4.5.8

Следует отметить, что значение коэффициента детерминации R² = 0.2227 свидетельствует о том, что выбранный вид уравнения регрессии (логарифмическая функция) не очень подходит к исходному заданию, так как максимальное значение коэффициента детерминации R² = 1.

На рис. 4.5.9 показан результирующий график использования в качестве уравнения регрессии логарифмической функции y = 1.59Ln(x) + 3.28 и построения линии тренда y =1.5852 Ln(x) + 3.2763для исходного варианта задания y = f(x).

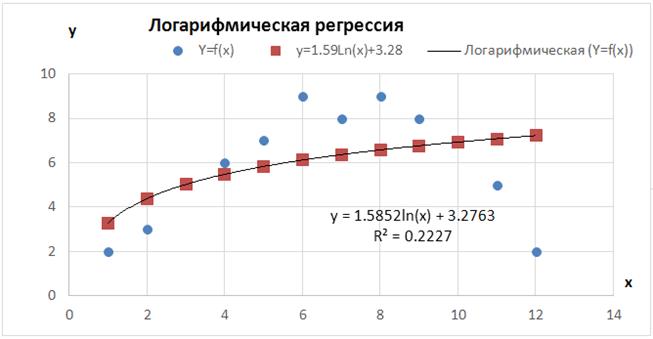
Рис. 4.5.9