Уравнение регрессии в виде гиперболы

В общем случае уравнение гиперболы имеет вид y = a/x + b.

Пусть исходная функция y = f(x) варианта задания имеет вид, показанный в таблице в диапазоне ячеек A7:B18, рис. 4.9.1.

Построим точечный график функции Гиперболическая регрессия y = f(x).

В строке 21 создадим шапку таблицы, как показано на рис. 4.9.1.

В ячейку B30 запишем произвольную константу 1, а в ячейку C30 - произвольную константу 2.

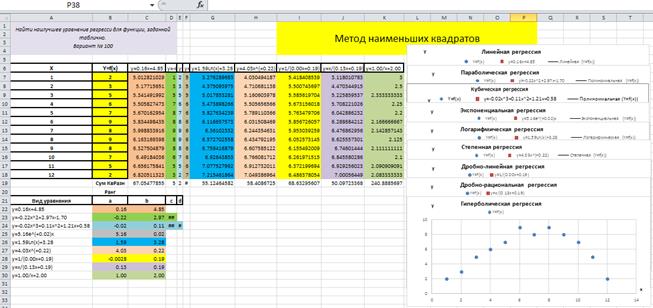
Рис. 4.9.1

В ячейку A30 запишем оператор присваивания для сцепленных символьных констант:

="y="&ТЕКСТ(B30;"0.00")&"/x"&ЕСЛИ(C30<0;ТЕКСТ(C30;"0.00");"+"&ТЕКСТ(C30;"0.00"))

Ячейке K6 присвоим такое же значение, какое приобретает ячейка A30, то есть K6 = A30.

Тогда, в соответствии с выбранными коэффициентами в ячейках B30=1 и C30=2, в ячейках A30 и K6получим результат y = 1.00/x + 2.00.

Запишем в ячейку K7 уравнение гиперболы с коэффициентами, взятыми в абсолютной адресации из ячеек B30 и C30, то есть =$B$30/A7+$C$30, в качестве аргумента X берётся значение ячейки A7исходной таблицы.

Скопируем закон преобразования информации ячейки K7 до ячейки K18 включительно.

В результате получим спектр значений функции y = 1/x + 2 на спектре аргументов X в диапазоне значений ячеек A7:A18, рис. 4.9.1.

В ячейку K19, используя мастер функций f_x, запишем результат вычисления функции =СУММКВРАЗН(B7:B18;K7:K18), рис. 4.9.2.

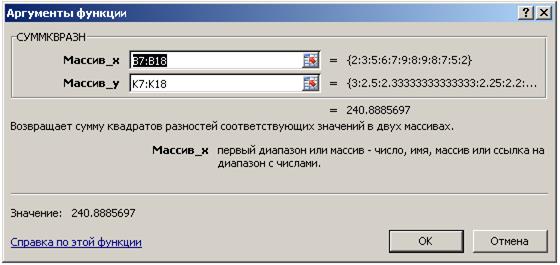
Рис. 4.9.2

Примечание: обозначение Массив_x и Массив_y, рис. 4.9.2, математическое и не совпадает с обозначениями выполняемого задания.

Добавим на точечный рисунок исходной таблицы уравнение гиперболы y = 1/x + 2, рис. 4.9.3.

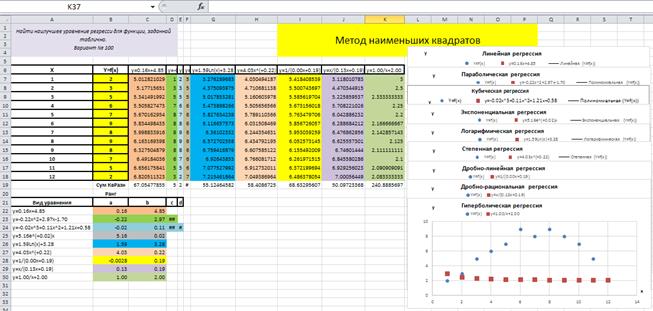
Рис. 4.9.3

Заметим, что это уравнение гиперболической регрессии, с произвольными значениями коэффициентов a=1 и b=2.

Соответствие этого уравнения регрессии исходному распределению оценено с помощью вычисления функции суммы квадратов разностей, значение которой составляет 240.8885697.

Для определения оптимальных значений коэффициентов a и b воспользуемся функцией Поиск решения:

– установим курсор в ячейку K19;

– последовательно, выбирая Разработчик, Данные, Поиск решения, вызвать окно Параметры поиска решения, в котором установить параметры, как показано на рис. 4.9.4, и нажать кнопку Найти решение;

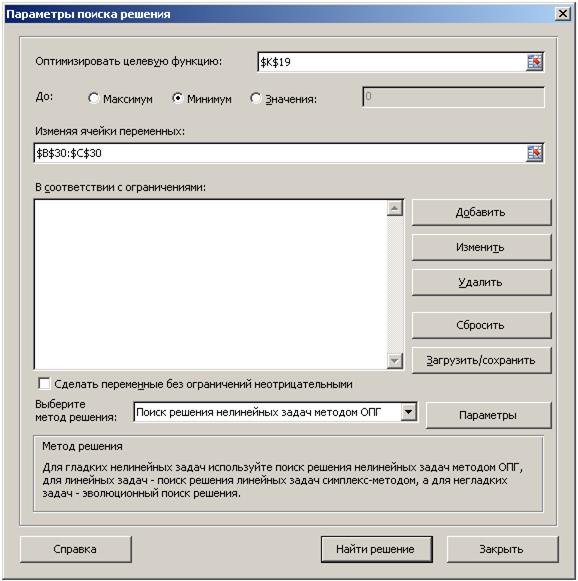
Рис. 4.9.4

– увидеть, как в ячейке B30 установится значение -5.66, в ячейке C30– 7.38, в ячейке K19 – 46.48573172, рис. 4.9.5;

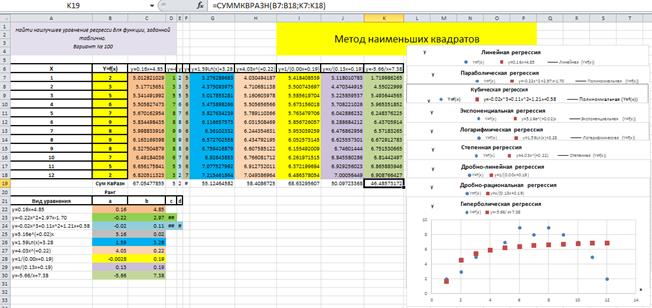
Рис. 4.9.5

Это означает, что гипербола с коэффициентами a =-5.66и b = 7.38отобразится на графике Гиперболическая регрессия, как показано на рис. 4.9.5, при этом значение суммы квадратов разностей будет минимально и равно 46.48573172.

Таким образом, коэффициенты для гиперболического уравнения регрессии определены и для исходного задания уравнение имеет вид y =-5.66/x + 7.38.

Так как в библиотеке линий тренда отсутствует гиперболическая функция, то проверить правильность решения добавлением линии тренда не представляется возможным.

На рис. 4.9.6 показан результирующий график использования в качестве уравнения регрессии гиперболической функции y =-5.66/x + 7.38для исходного варианта задания y = f(x).

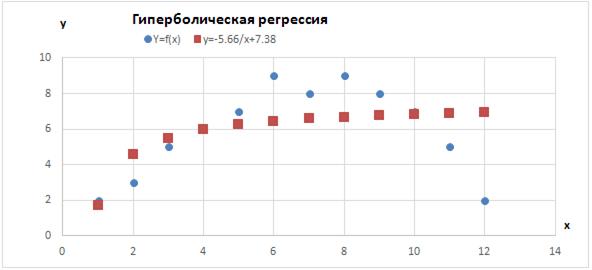
Рис. 4.9.6

Оценка результатов

Для оценки полученных результатов, то есть для определения уравнения регрессии наилучшим образом соответствующего исходному табличному заданию функции y = f(x) необходимо сравнить рассмотренные уравнения регрессии по вычисленным значениям сумм квадратов разностей или по значениям коэффициентов детерминации. Значения сумм квадратов разностей находятся в ячейках C19:K19.

При выполнении сравнения целесообразно использовать имеющуюся в среде Excel функцию РАНГ.

Для чего:

– установить курсор в ячейку B20и записать в неё символьную константу “Ранг”, рис. 4.10.1;

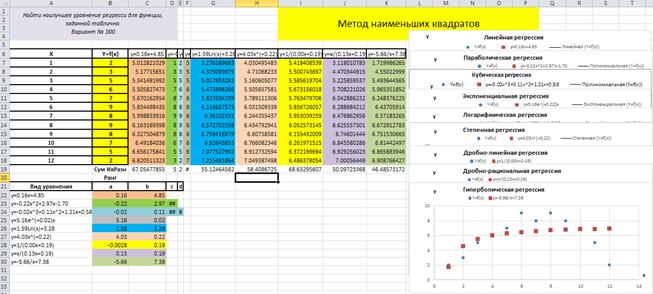
Рис. 4.10.1

– установить курсор в ячейку C20и вызвать с помощью мастера функций f_x функцию РАНГ, рис. 4.10.2, (столбцы D, C и F сжаты);

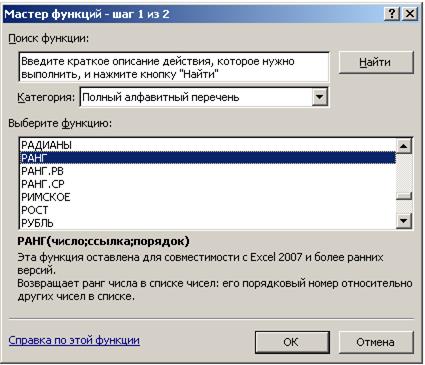
Рис. 4.10.2

– в появившемся окне Аргументы функции в окне Число ввести адрес ячейки C19, в окне Ссылка ввести диапазон ячеек $C$19:$K$19, в окне Порядок ввести константу, например, 2 и нажать кнопку ОК, рис. 4.10.3;

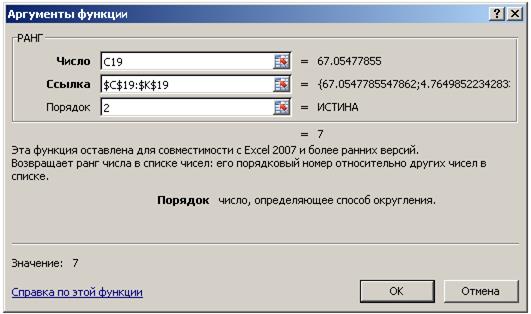
Рис. 4.10.3

Адрес ячейки C19 указывается потому, что в этой ячейке находится число, в данном случае это 67.05477855, место которого (Ранг) мы хотим определить среди всех чисел, находящихся в ячейках диапазона $C$19:$K$19 (обязательно указывать в абсолютной адресации).

Константа 2 определяет порядок ранжирования по убыванию или по возрастанию, в данном случае на первое место (Ранг 1) помещается самое маленькое число.

– в ячейке C20появится число 7, это означает, что число 67.05477855занимает седьмое место (имеет ранг 7) по возрастанию среди всех чисел диапазона ячеек $C$19:$K$19, рис. 4.10.4;

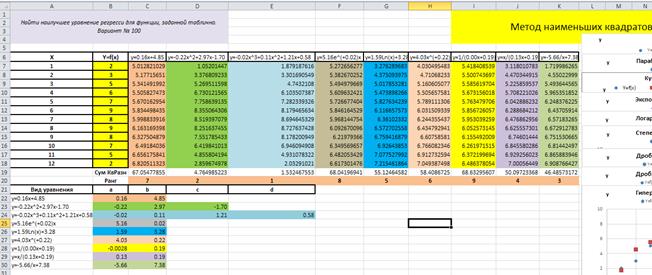
Рис. 4.10.4

– скопировать функцию Ранг ячейки C20 на весь диапазон ячеек C20:K20, в результате получим значения рангов для всех чисел, находящихся в диапазоне ячеек $C$19:$K$19, рис. 4.10.4.

Для удобства результаты ранжирования можно объединить в таблицу, рис. 4.10.5.

Рис. 4.10.5

Исходя из таблицы рис. 4.10.5, можно сделать вывод о том, что для рассмотренного варианта задания из всех девяти исследованных уравнений регрессии исходному табличному заданию функции y = f(x)наилучшим образом соответствует уравнение кубического полинома y=-0.02x³+0.11x²+1.21x+0.58, так как вычисленная для него сумма квадратов разностей имеет минимальное значение 1.532467553.

Этот результат подтверждается и значением коэффициента детерминации, величина которого 0.9784, то есть максимальна.

Результат выполнения заданного варианта показан на рис. 4.10.6.

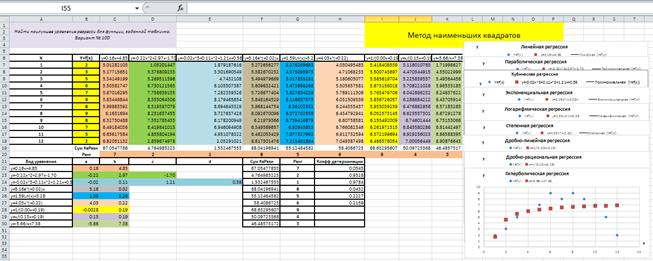
Рис. 4.10.6

Рекомендуемая литература

1. Никифоров С.Н., Информатика для I курса. Ч. I: учебное пособие по выполнению лабораторных работ по курсу “Информатика”, СПбГАСУ, СПб., 2011. – 100 c.

2. Никифоров С.Н., Информатика для I курса. Ч. II: учебное пособие по выполнению лабораторных работ по курсу “Информатика”, СПбГАСУ, СПб., 2015. – 100 c.

3. Гарнаев А. Ю., Использование MS Excel и VBA в экономике и финансах, СПб.: БХВ – Санкт-Петербург, 1999. – 336 с., ил.

4. Гарбер Г.З. Основы программирования на Visual Basic и VBA в Excel 2007, Москва, Солон-Пресс, 2008, 192 с.

[1] Криволинейная трапеция – такая трапеция, у которой одна сторона отрезок параболы.

[2] Если раздел Разработчик отсутствует, то добавить его, пройдя по цепочке Файл, Параметры, Настройка ленты, Разработчик

[3] Если раздел Поиск решенияотсутствует, то добавить его, пройдя по цепочке Разработчик, Надстройки, Поиск решения

[4] Коэффициент детерминации