Конструктивные или генетические определения

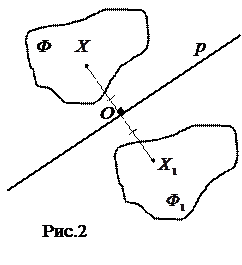В конструктивных определениях содержание понятия раскрывается посредством описания происхождения объекта или способа его образования. Например, «корнем п-ой степени из числа а называется такое число, п-ая степень которого равна а» или «степенью числа а с натуральным показателем п (п≠1) называется произведение п множителей, каждый из которых равен а». В геометрии: «пусть F - данная фигура и р – фиксированная прямая. Возьмём произвольную точку Х фигуры и опустим перпендикуляр ХО на прямую р. На продолжении перпендикуляра за точку О отложим отрезок 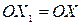. Преобразование фигуры Ф в фигуру 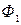, при котором каждая точка Х переходит в точку 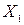, построенную указанным образом, называется симметрией

относительно прямой р».

«Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым».

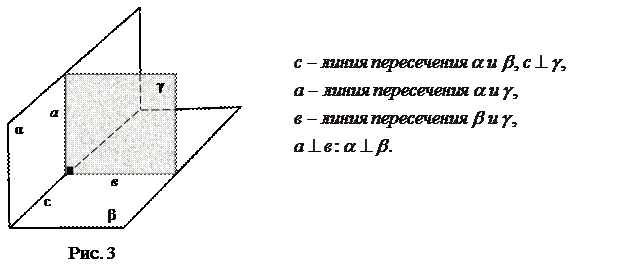
Иногда определение является классическим, но видовое отличие описывается конструктивно. Например, «пирамидой называется многогранник (род), который состоит из плоского многоугольника - основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания».

Частным случаем генетических определений являются индуктивные определения, в которых указываются некоторые базисные элементы и правило, позволяющее получать новые элементы из уже имеющихся. Так, например, арифметическую прогрессию можно определить посредством двух чисел 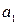, d и правила 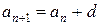(числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом).

Перечисленные определения понятий относятся к так называемым явным. В них может быть выявлено определяемое и определяющее понятия. Однако определяющее понятие ранее также являлось определяемым. Например, в цепочке понятий «квадрат → ромб → параллелограмм →

четырёхугольник → многоугольник → геометрическая фигура → множество точек» каждое предыдущее понятие определяется через следующее. Такую цепочку называют родословной понятия. Ясно, что она не может быть бесконечной. Последние понятия в ней «множество», «точка» не определяются (так называемые основные понятия). Их свойства описываются в системе аксиом теории. Аксиомы рассматриваются как неявные определения основных понятий.