Переходные процессы в асинхронном электроприводе с нелинейными механическими характеристиками
Зависимости 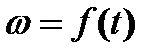 или
или 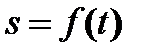 являются нелинейными и могут быть рассчитаны по формуле Клосса
являются нелинейными и могут быть рассчитаны по формуле Клосса
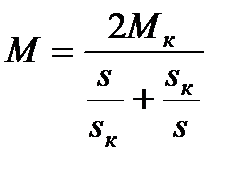 ,
,
где 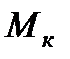 и
и 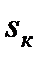 критический момент и критическое скольжение,
критический момент и критическое скольжение,
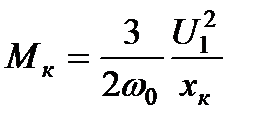 ;
;
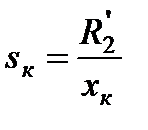 .
.
На рис. 7.11 представлена схема прямого пуска асинхронного двигателя с короткозамкнутым ротором и механические характеристики при пуске.
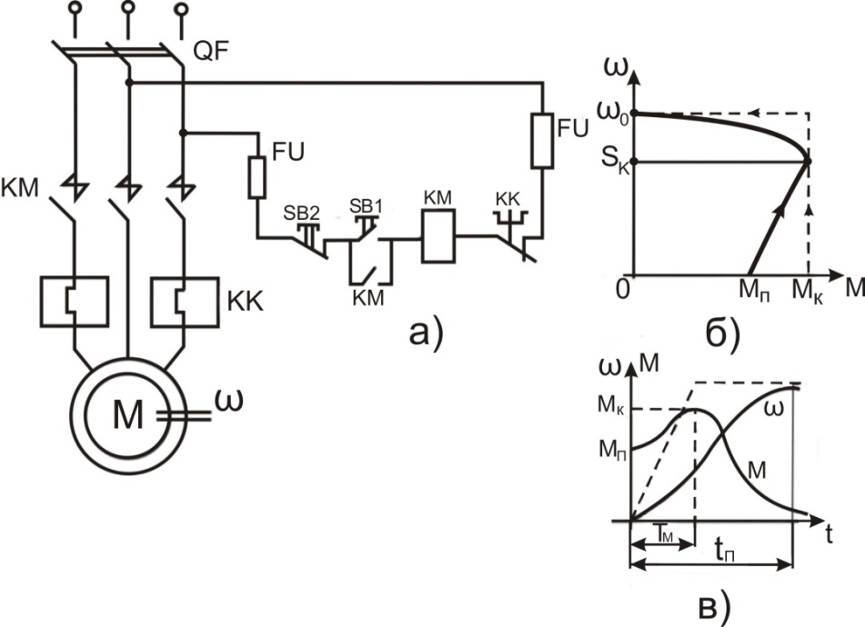
Рис. 7.11. Схема (а) и механическая характеристика (б), графики переходных процессов (в)
Принципиальная схема (рис. 7.11,а) содержит асинхронный короткозамкнутый двигатель М с моментом инерции J, автоматический выключатель QF, трехфазный линейный контактор KM, две кнопки SB1 (пуск) и SB2 (стоп), тепловое реле KK, плавкие предохранители FU. Контактор и тепловое реле обычно конструктивно объединены в одном аппарате – магнитном пускателе.
Нажатием кнопки SB1 при включенном QF катушка контактора KM получает питание, замыкаются контакты KM в силовой цепи статора и к обмотке статора подводится напряжение сети. Двигатель разгоняется по характеристике 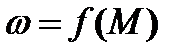 (рис. 7.11,б), включенный контакт КМ заблокирует кнопку SB1, тем самым обеспечивая питание катушки КМ после отпускания кнопки SB1.
(рис. 7.11,б), включенный контакт КМ заблокирует кнопку SB1, тем самым обеспечивая питание катушки КМ после отпускания кнопки SB1.
Нажатие на кнопку SB2 обесточивает катушку контактора КМ, двигатель отключается от сети и тормозится моментом статической нагрузки 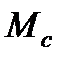 или находится на свободном выбеге.
или находится на свободном выбеге.
Защита от перегрузки осуществляется автоматически выключателем QF, который должен отстроен от пускового тока; от тепловой перегрузки и обрыва фазы – с помощью теплового реле КК.
Это простейшая схема, осуществляющая только пуск двигателя; в справочниках можно найти варианты этой схемы с добавленными функциями – динамического торможения, торможения противовключением и реверса.
Переходные функции 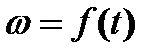 ,
, 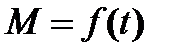 в режимах пуска, торможения и реверса, несмотря на нелинейность
в режимах пуска, торможения и реверса, несмотря на нелинейность 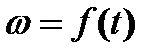 , можно рассчитать и построить аналитическим методом; кроме того можно произвести анализ влияния сопротивления роторной цепи
, можно рассчитать и построить аналитическим методом; кроме того можно произвести анализ влияния сопротивления роторной цепи 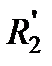 на показатели переходного процесса.
на показатели переходного процесса.
Для упрощения математических выкладок при решении поставленной задачи принимается, что в переходных процессах 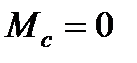 . тогда уравнение движения электропривода может быть представлено в следующем виде
. тогда уравнение движения электропривода может быть представлено в следующем виде
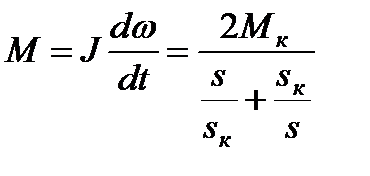 , (7.26)
, (7.26)
а с учётом, что
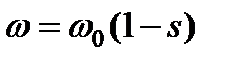 ;
;
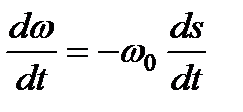 ,
,
получим
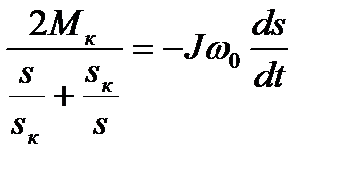 .
.
Решая это уравнение относительно времени, можно записать
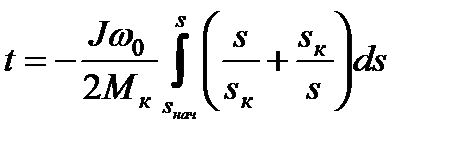 .
.
После интегрирования окончательное выражение для определения времени переходного процесса пуска, торможения, реверса может быть представлено в относительных единицах 
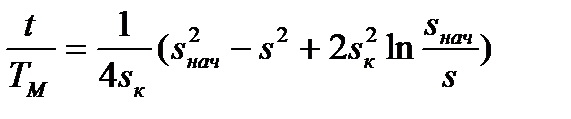 , (7.27)
, (7.27)
Физический смысл 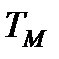 – это время, в течении которого асинхронный двигатель разгонится из неподвижного состояния до скорости
– это время, в течении которого асинхронный двигатель разгонится из неподвижного состояния до скорости 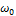 под действием неизменного критического момента
под действием неизменного критического момента 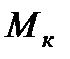 , что наглядно поясняется графиками (штриховыми линиями) на рис. 7.11,б.
, что наглядно поясняется графиками (штриховыми линиями) на рис. 7.11,б.
Рассмотрим на примерах количественные соотношения в переходных процессах асинхронного электропривода без учёта электромагнитной инерции.
Пример 1. Переходные процессы при пуске ( 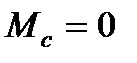 )
)
В этом случае 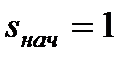 ,
, 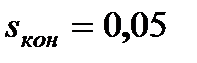 (см. рис. 7.11,б), время пуска после подстановки этих значений в уравнение (7.27) определится
(см. рис. 7.11,б), время пуска после подстановки этих значений в уравнение (7.27) определится 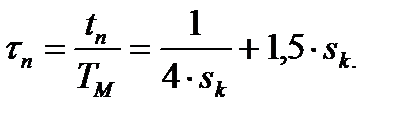 (7.28)
(7.28)
Эта функция 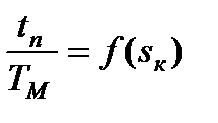 имеет экстремум. Производная от функции (7.28)
имеет экстремум. Производная от функции (7.28)
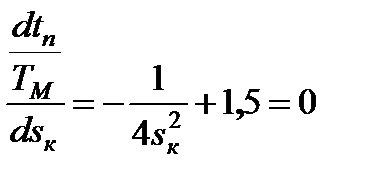 ,
,
откуда оптимальное критическое скольжение, при котором 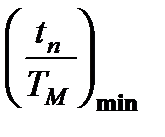 ,
,
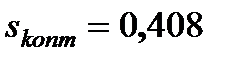 .
.
После подстановки этого значения в формулу (7.28) имеем
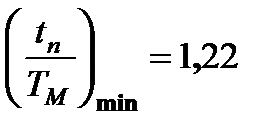 ,
,
т.е. минимальное время пуска при 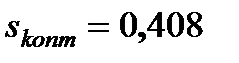 всего на 22% больше
всего на 22% больше 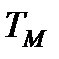 . Момент пусковой эффективный
. Момент пусковой эффективный
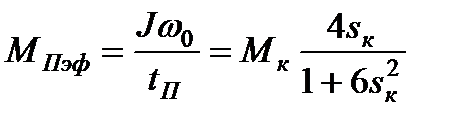 .
.
При 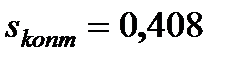
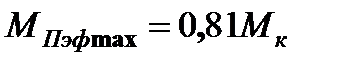 .
.
Таким образом, для электроприводов, работающих с частыми пусками, необходимо применять асинхронные двигатели с повышенным критическим скольжением ( 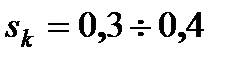 ).
).
Пример 2. Переходные процессы при торможении противовключением ( 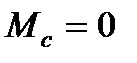 ).
).
Для осуществления торможения противовключением необходимо изменить чередование фаз с А,В,С, например, на В,А,С . При этом момент двигателя становится тормозным
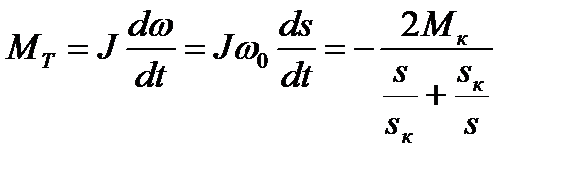 , (7.29)
, (7.29)
где
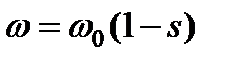 ;
;
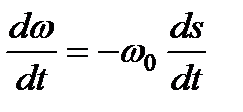 .
.
Решая уравнение (7.29) относительно времени t, получим
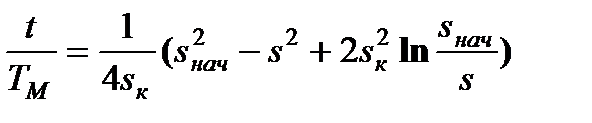
т.е. такое же выражение (7.27), что и при пуске.
При подстановке в последнее уравнение 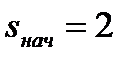 ,
, 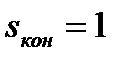 получим
получим
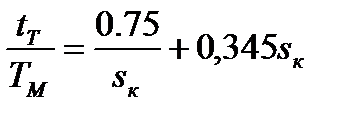 . (7.30)
. (7.30)
производная от (7.30)
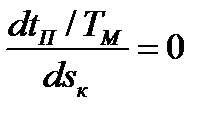
позволяет определить
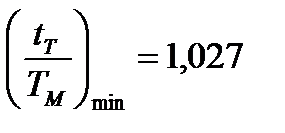 при
при 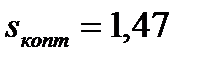 .
.
Тогда момент тормозной эффективный
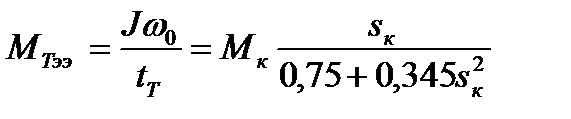 . (7.31)
. (7.31)
При 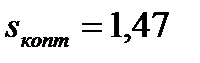
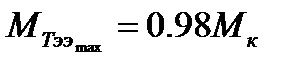 .
.
Зависимости, представленные на рис. 7.12,б и 7.12,в, соответствуют 1 - 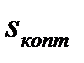 = 0,408; 2 -
= 0,408; 2 - 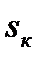 =0,2; 3 -
=0,2; 3 - 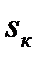 =0,8.
=0,8.
Методика расчёта переходных процессов такая же, что и при пуске.
Пример 3. Динамическое торможение ( 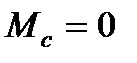 )
)
Как известно, для осуществления динамического торможения асинхронного электропривода статор двигателя отключается от сети переменного тока и в его обмотку подаётся постоянный ток.
 Рис. 7.12 Зависимости
Рис. 7.12 Зависимости 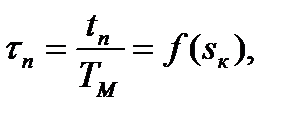
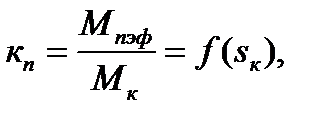
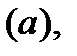
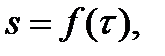
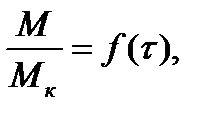
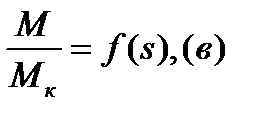
Для ненасыщенного двигателя справедливо уравнение механической характеристики, совпадающее по виду с упрощенной формулой Клосса (5.50)
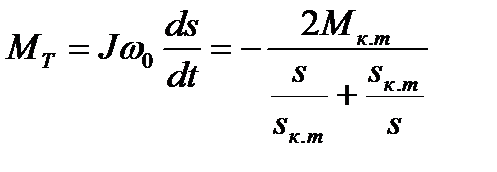 . (7.32)
. (7.32)
Время торможения
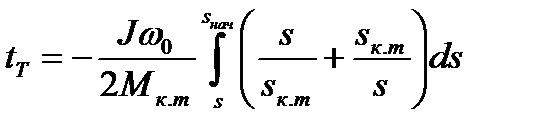 ,
,
тогда после интегрирования в пределах от 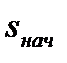 до
до 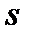 получим
получим
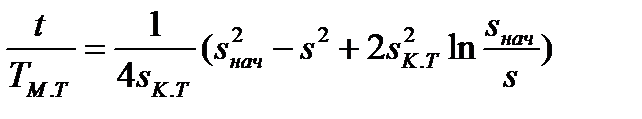 , (7.33)
, (7.33)
где 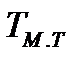 - электромеханическая постоянная времени электропривода при динамическом торможении;
- электромеханическая постоянная времени электропривода при динамическом торможении;
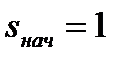 - начальное скольжение при торможении
- начальное скольжение при торможении
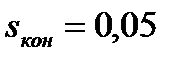 - конечное скольжение.
- конечное скольжение.
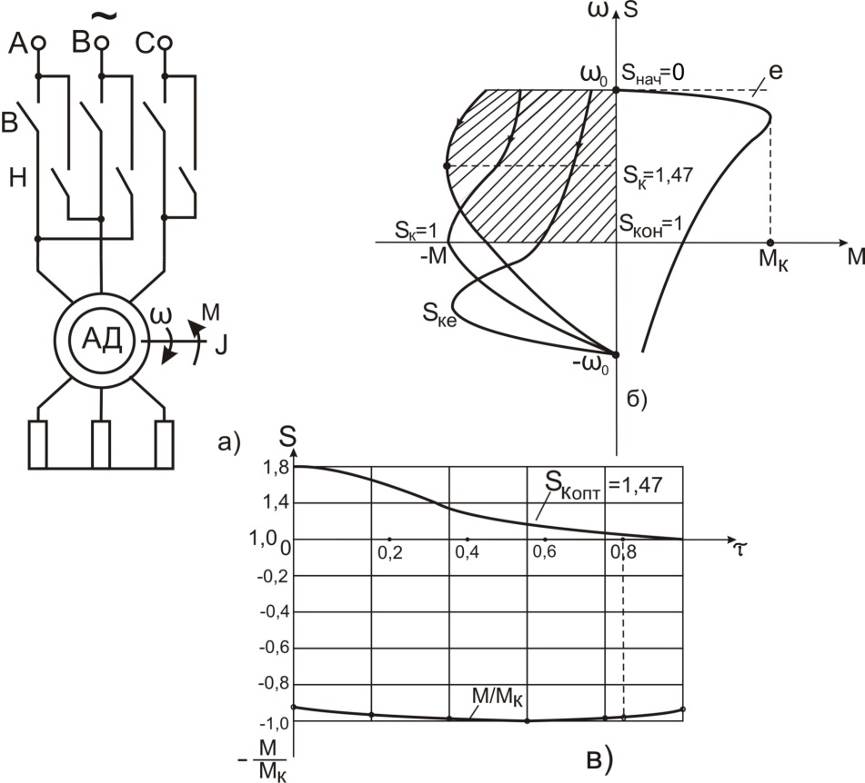
Рис. 7.13. Схема (а), механические характеристики (б) и переходные процессы при 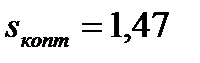 (в)
(в)
Окончательно время торможения определится
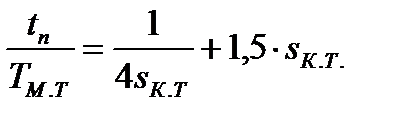 .
.
Минимальное время торможения составляет 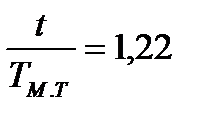 при критическом скольжении
при критическом скольжении 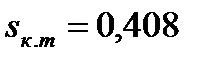 .
.
Так как критическое скольжение при динамическом торможении асинхронных двигателей с короткозамкнутым ротором значительно меньше, чем значения в двигательном режиме, можно принять, что
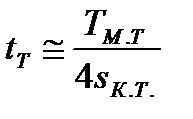 . (7.34)
. (7.34)
Этой формулой удобно воспользоваться при решении обратной задачи: по заданному времени торможения 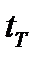 определить критический момент
определить критический момент
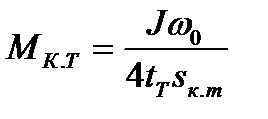
а по формуле
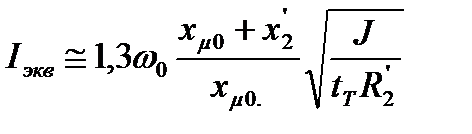 , (7.35)
, (7.35)
найти эквивалентный ток статора, который связан с величиной постоянного тока, подаваемого в статор
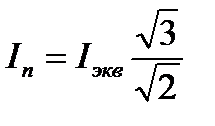 при соединении обмотки статора в звезду,
при соединении обмотки статора в звезду,
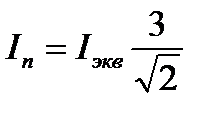 при соединении обмотки статора в треугольник.
при соединении обмотки статора в треугольник.
Кроме того, если учесть, что индуктивное сопротивление намагничивающего контура 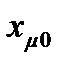 <<
<< 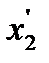 , формулу (7.35) можно представить в виде
, формулу (7.35) можно представить в виде
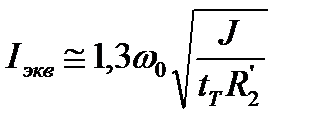 .
.
Переходные функции 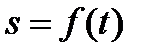 ,
, 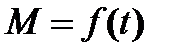 рассчитываются по той же методике, что и при пуске, и торможении противовключением.
рассчитываются по той же методике, что и при пуске, и торможении противовключением.
Математическое описание переходных процессов при 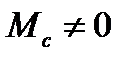 несколько сложнее и может быть представлено в следующем виде:
несколько сложнее и может быть представлено в следующем виде:
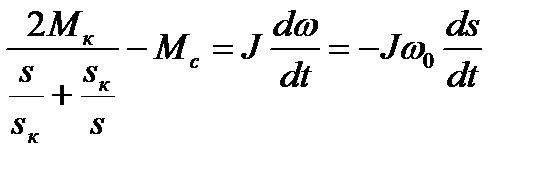 ; (7.36)
; (7.36)
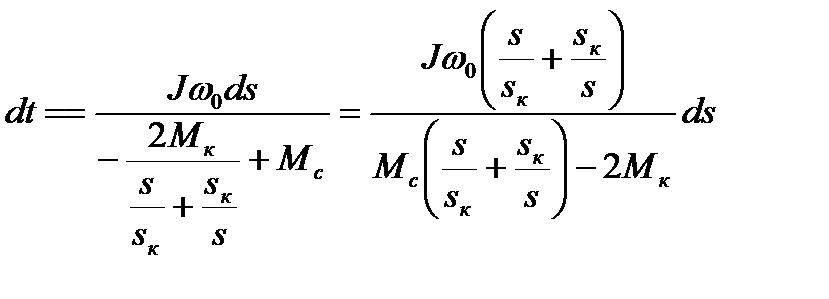 .
.
После некоторых преобразований получим
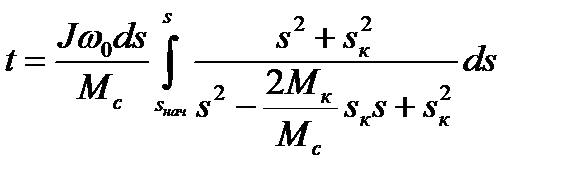 . (7.37)
. (7.37)
Полученный интеграл находится методом разложения на элементарные дроби и после интегрирования и подстановки пределов относительное время переходного процесса определится так
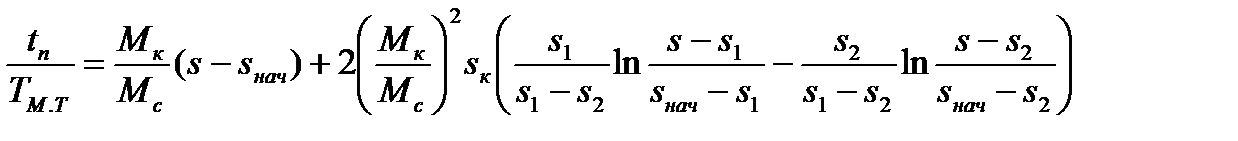 ,
,
где 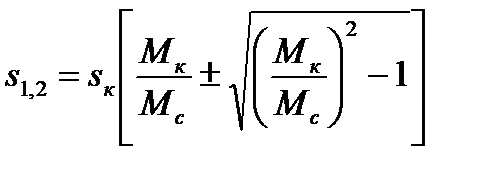 ;
;
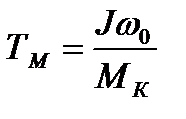 .
.
Приближённо время пуска, торможения можно определить по формулам
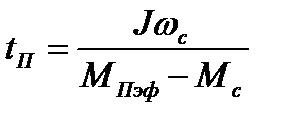 ;
; 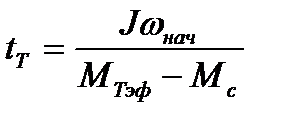 .
.
Дата добавления: 2019-02-08; просмотров: 1567;











