Переходные процессы в разомкнутых электроприводах
Общие сведения
Переходным процессом электропривода называется режим его работы при переходе из одного установившегося состояния к другому, при этом изменяются координаты электропривода: скорость, токи, момент, магнитный поток двигателя. Это зависимости 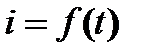 ,
, 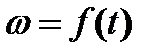 ,
, 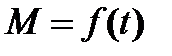 ,
, 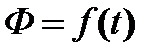 .Анализ этих зависимостей позволяет определить характер переходного процесса (монотонный или колебательный), время переходного процесса; определить допустимость возникающих в динамических режимах величин момента, ускорения, тока, которые определяют механические и электрические перегрузки в электроприводе; произвести правильный выбор мощности двигателя и аппаратуры управления.
.Анализ этих зависимостей позволяет определить характер переходного процесса (монотонный или колебательный), время переходного процесса; определить допустимость возникающих в динамических режимах величин момента, ускорения, тока, которые определяют механические и электрические перегрузки в электроприводе; произвести правильный выбор мощности двигателя и аппаратуры управления.
Без переходных процессов не совершается движение ни одного электропривода, в простейшем случае, например, в электроприводе вентилятора, транспортёра, требуется осуществить пуск двигателя. При этом мгновенное подключение напряжения к обмоткам двигателя не приводит к скачкообразному изменению скорости, а осуществляется изменение скорости, тока, момента двигателя во времени. Большому количеству электроприводов механизмов присущи переходные процессы при электрическом торможении двигателя: рекуперативном, противовключением, динамическом.
Переходные процессы возникают при регулировании скорости, когда двигатель переводится с одной скорости на другую, например, изменением сопротивления, напряжения, потока и частоты.
Ряд механизмов, таких как кривошипно-шатунные (механизм качания кристаллизатора, ножницы и т.п.) характеризуются пульсирующем изменением нагрузки на валу двигателя. Такие механизмы не имеют установившегося режима, а их электропривод имеет периодические переходные процессы.
Переходные процессы пуска и торможения могут быть не редкими явлениями, а основными рабочими режимами, например, в электроприводах реверсивных прокатных станов, рабочих рольгангов, механизмов поворота экскаватора и т.д. Эти процессы, а также процессы регулирования скорости возникают регулярно путём воздействия оператора или автоматически в соответствии с технологическим процессом работы механизма. Переходные процессы могут возникать также при набросе и сбросе нагрузки, колебаниях напряжения сети, частоты сети и т.д.
Итак, внешней причиной, вызывающей переходный процесс в электроприводе, являются управляющие и возмущающие воздействия. Управляющие воздействия это напряжение, напряжение и его частота, сопротивление в цепях двигателя, магнитный поток; возмущающие воздействия – изменение момента нагрузки на валу двигателя, момента инерции электропривода, колебания напряжения сети, частоты и т.д. Эти воздействия являются побуждающими электропривод к переходному процессу. Реакция электропривода на управляющее или возмущающее воздействие составляет суть переходных процессов. Внутренней причиной переходных процессов являются инерционности электропривода – механическая и электромагнитная инерционности. Изменение запаса кинетической энергии в механической части электропривода и электромагнитной энергии в электрической части привода происходит постепенно, что и объясняет возникновение переходных процессов.
Все возникающие задачи по исследованию переходных процессов в электроприводах разделяются на четыре больших группы.
1.Преобладающей инерционностью в приводе является механическая инерционность (момент инерции 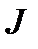 ); электромагнитные инерционности (индуктивность L) малы или не проявляются. Фактор, вызывающий переходный процесс, изменяется скачкообразно (мгновенно), т.е. намного быстрее, чем скорость.
); электромагнитные инерционности (индуктивность L) малы или не проявляются. Фактор, вызывающий переходный процесс, изменяется скачкообразно (мгновенно), т.е. намного быстрее, чем скорость.
Примеры таких задач: мгновенный наброс и сброс нагрузки, пуск, торможение, реверс, регулирование скорости асинхронных двигателей и двигателей постоянного тока при Ф=const.
2.Преобладающая инерционность – механическая ( 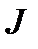 ); индуктивности (L) электрических цепей малы или не проявляются. Фактор, вызывающий переходный процесс, изменяется во времени и темп этого изменения соизмерим с темпом изменения скорости.
); индуктивности (L) электрических цепей малы или не проявляются. Фактор, вызывающий переходный процесс, изменяется во времени и темп этого изменения соизмерим с темпом изменения скорости.
Примеры таких задач: переходные процессы в системах ТП-Д, ПЧ-АД, если L=0.
3.Механическая ( 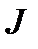 ) и электромагнитная (L) инерционность соизмеримы; фактор, вызывающий переходный процесс, – изменяется мгновенно.
) и электромагнитная (L) инерционность соизмеримы; фактор, вызывающий переходный процесс, – изменяется мгновенно.
Примеры: переходные процессы в электроприводах постоянного тока при Ф=var; то же при Ф= const, но L 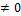 .
.
4.Учитывается несколько инерционностей, фактор, вызывающий переходный процесс, изменяется не мгновенно. Это наиболее сложные задачи, относящиеся к замкнутым системам электроприводов (изучаются в специальных курсах).
7.2.2. Переходные процессы в электроприводах с линейными механическими характеристиками при 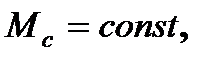
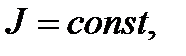
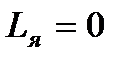 и быстрых изменениях воздействующего фактора
и быстрых изменениях воздействующего фактора
Примерами таких электроприводов являются: электропривод постоянного тока с двигателем независимого (параллельного) возбуждения с линейной механической характеристикой (рис. 7.5,а), с двигателями параллельного и смешанного возбуждения с линеаризованными механическими характеристиками (рис. 7.5,б), с асинхронными двигателями при работе на характеристиках при 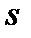 <
< 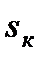 (рис. 7.5,в), (сплошные линии).
(рис. 7.5,в), (сплошные линии).
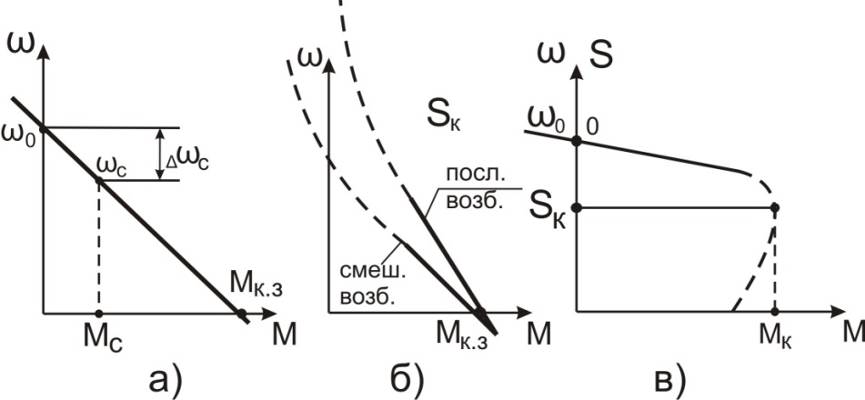
Рис. 7.5. Линейные и линеаризованные характеристики электроприводов
Рассмотрим на примере электропривода с ДПТ НВ переходные процессы при быстрых изменениях управляющего воздействия (подводимого напряжения или дополнительных сопротивлений в якорной цепи). Принципиальная схема включения двигателя представлена на рис. 7.6.
Предлагается следующее математическое описание переходных процессов для рассматриваемого электропривода.
В его основе лежат два уравнения: уравнение равновесия силовых цепей, составленное по второму закону Кирхгофа,
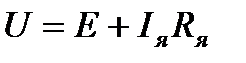 (7.14)
(7.14)
и уравнение движения механической части электропривода
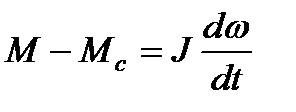 . (7.15)
. (7.15)
С учётом того, что 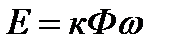 , а
, а 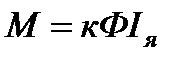 , совместное решение уравнений (7.14) и (7.15) даёт дифференциальное уравнение
, совместное решение уравнений (7.14) и (7.15) даёт дифференциальное уравнение
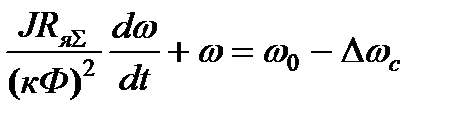 .(7.16)
.(7.16)
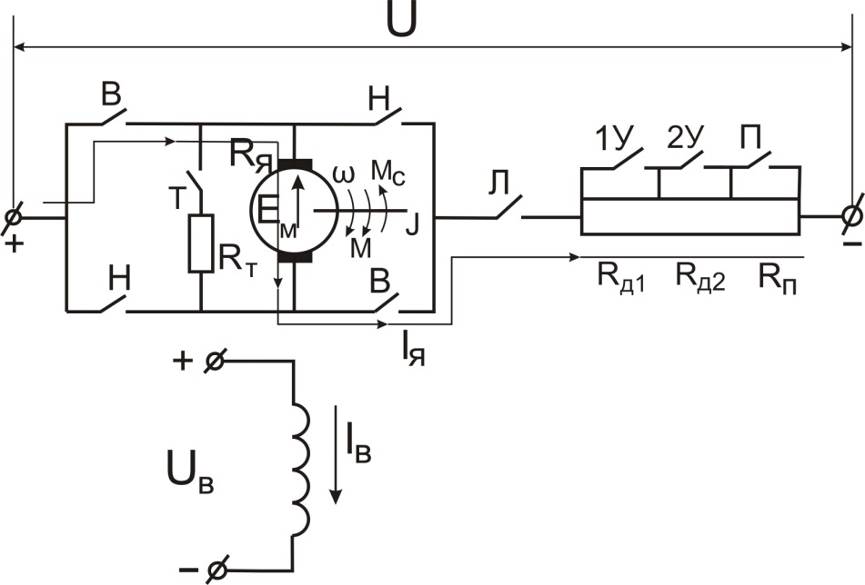 Рис. 7.6. Принципиальная схема электропривода с ДПТ НВ
Рис. 7.6. Принципиальная схема электропривода с ДПТ НВ
где 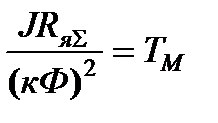 - электромеханическая постоянная времени электропривода;
- электромеханическая постоянная времени электропривода;
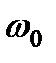 – скорость идеального холостого хода;
– скорость идеального холостого хода; 
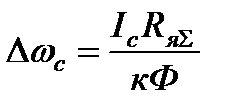 – статическое падение скорости.
– статическое падение скорости.
Тогда уравнение (7.16) с учётом, что 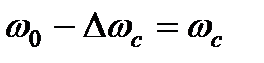 (установившееся значение скорости), получим дифференциальное уравнение
(установившееся значение скорости), получим дифференциальное уравнение
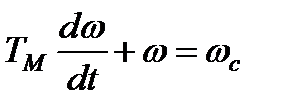 , (7.17)
, (7.17)
решение которого имеет следующий вид
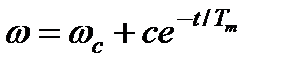 ,
,
где С – постоянная интегрирования, находится из начальных условий.
При t=0, 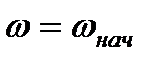 ,
, 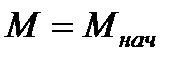 ,
, 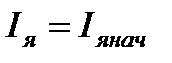 .Тогда
.Тогда 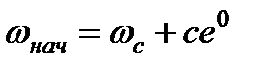 и
и 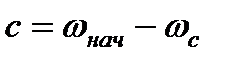 , а решение дифференциального уравнения (7.17) запишется в виде
, а решение дифференциального уравнения (7.17) запишется в виде
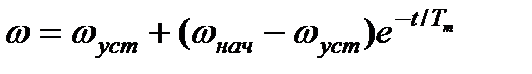 . (7.18)
. (7.18)
Так как  линейная зависимость, то уравнение относительно момента можно записать в виде
линейная зависимость, то уравнение относительно момента можно записать в виде
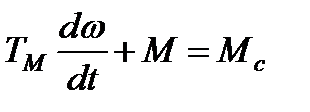 ,
,
а его решение может быть представлено в виде
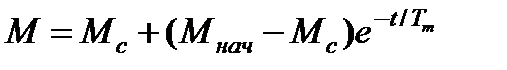 . (7.19)
. (7.19)
На рис.7.7 представлены механические характеристики двигателя и механизма, а также графики переходных процессов 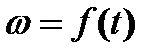 ,
, 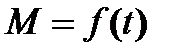 , в общем случае при ненулевых начальных условиях, рассчитанные по уравнениям (7.18) и (7.19).
, в общем случае при ненулевых начальных условиях, рассчитанные по уравнениям (7.18) и (7.19).
Коэффициент при производной в дифференциальных уравнениях (7.17) и (7.19)
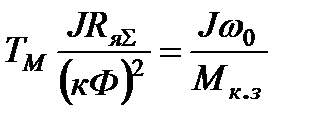
называют электромеханической постоянной времени.
Для пояснения физического смысла этой постоянной времени рассмотрим случай, когда 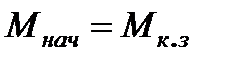 а конечная скорость
а конечная скорость 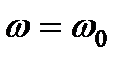 , т.е. привод разгоняется с неизменным моментом
, т.е. привод разгоняется с неизменным моментом 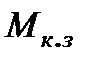 . Тогда электромеханическая постоянная времени это есть время, за которое привод разогнался бы вхолостую до скорости
. Тогда электромеханическая постоянная времени это есть время, за которое привод разогнался бы вхолостую до скорости 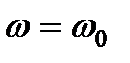 под действием неизменного момента, равного моменту короткого замыкания.
под действием неизменного момента, равного моменту короткого замыкания.
Рассмотрим несколько примеров по расчёту и анализу переходных процессов при пуске, торможении противовключением, динамическом торможении и при реверсе.
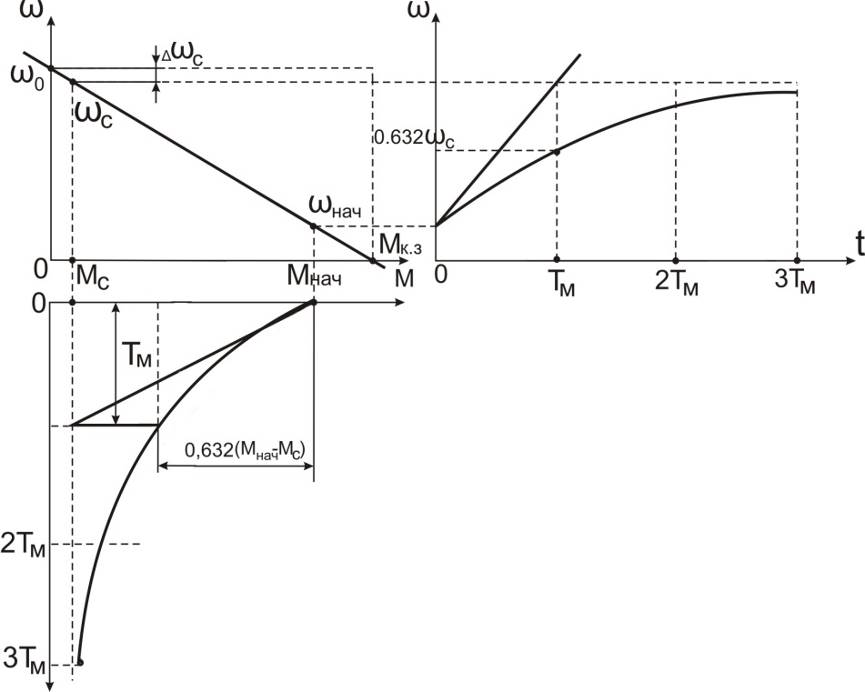
Рис. 7.7. Механические характеристики и графики переходных процессов 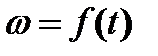 ,
, 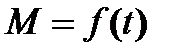 .
.
Пример 1. Пуск двигателя по реостатной характеристике (схема на рис. 7.6)
На основании (7.18) и (7.19) можно записать переходные функции 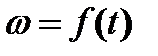 ,
, 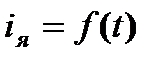 следующим образом
следующим образом
при 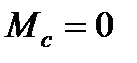
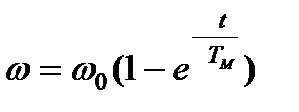 ;
;
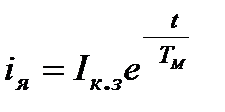 ;
;
при 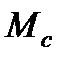 реактивном и активном, но в сторону подъёма груза
реактивном и активном, но в сторону подъёма груза
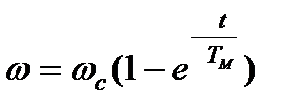 ;
;
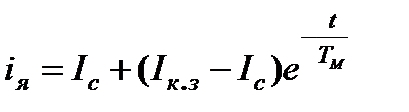 ;
;
при 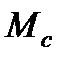 активном, но пуск в сторону опускания груза
активном, но пуск в сторону опускания груза
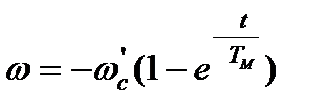 ;
;
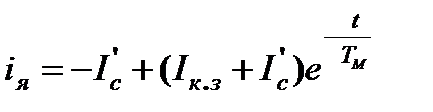 .
.
Как следует из приведённых функций и графиков переходных процессов (рис. 7.8), время пуска определяется путём решения переходных функций относительно времени t, а именно
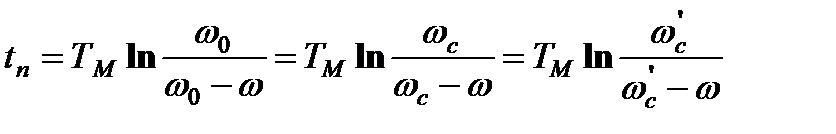 ,,
,,
и после подстановки в них текущего значения скорости, равного 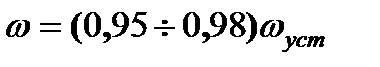 , получим
, получим 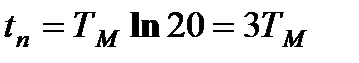 ,
, 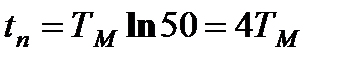 .
.
Пример 2. Торможение противовключением и реверс двигателя
В соответствии со схемой включения двигателя (рис. 7.6) торможение электропривода и последующий реверс осуществляется сменой полярности напряжения U, подводимого к якорю двигателя. При этом в цепи якоря отключаются контакты контактора «В» и замыкаются контакты «Н», а в цепь якоря вводятся сопротивления 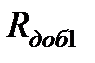 ,
, 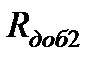 и ступень противовключения
и ступень противовключения 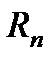 . Суммарное сопротивление якорной цепи определяется
. Суммарное сопротивление якорной цепи определяется
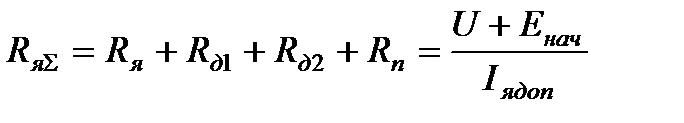 .
.
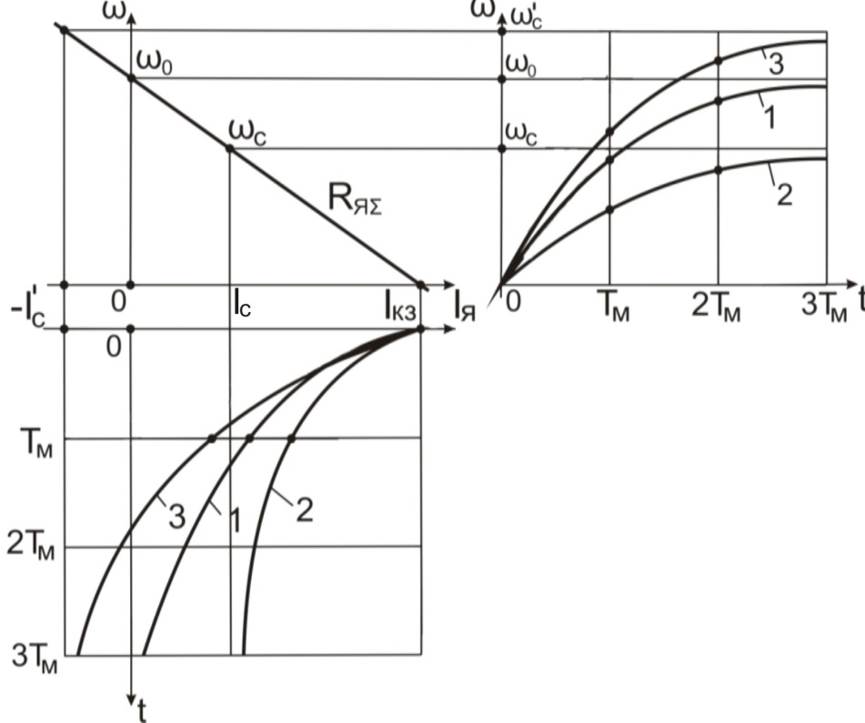
Рис. 7.8. Переходные процессы при пуске вхолостую (1- 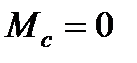 ), при пуске под нагрузкой (2 -
), при пуске под нагрузкой (2 - 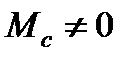 ), при пуске с активным моментом (3-
), при пуске с активным моментом (3- 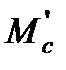 <0)
<0)
Если задаться током 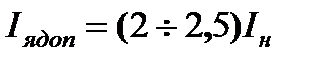 , то внешнее сопротивление, введённое в якорную цепь, определится по формуле
, то внешнее сопротивление, введённое в якорную цепь, определится по формуле
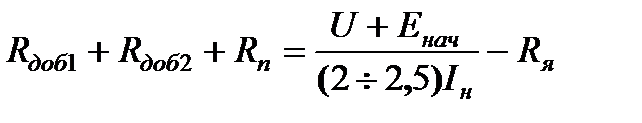 ,
,
где 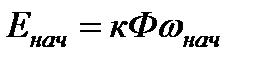 - начальное значение ЭДС двигателя.
- начальное значение ЭДС двигателя.
Решение задачи начнём с построения механических характеристик 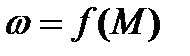 (рис. 7.8,а), на котором
(рис. 7.8,а), на котором 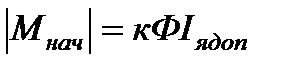 .
.
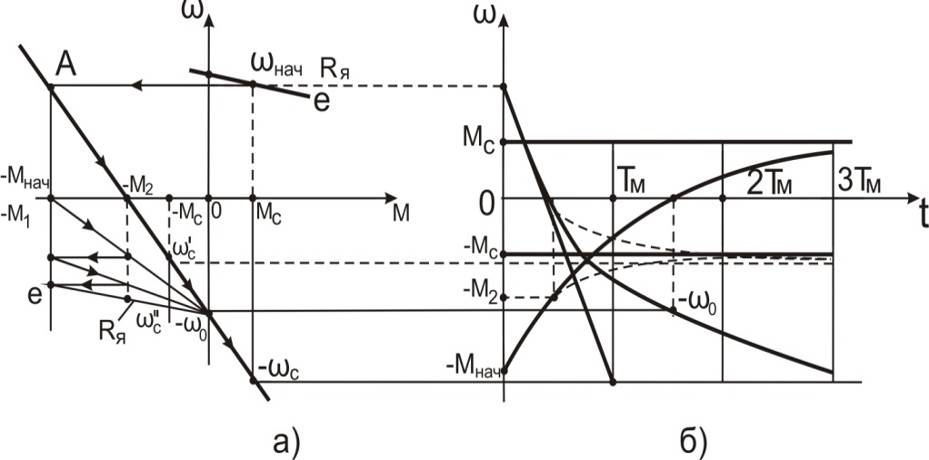
Рис.7.9. Механические (а) и переходные функции (б)
Переходный процесс торможения противовключением протекает одинаково как с активным, так и с реактивным моментом статических сопротивлений 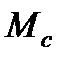 в координатах для скорости от
в координатах для скорости от 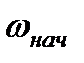 до (-
до (- 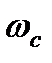 ), а момента – от (
), а момента – от ( 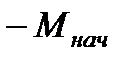 ) до
) до 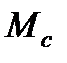 . Тогда в соответствии с уравнениями (7.18) и (7.19) переходные функции имеют вид
. Тогда в соответствии с уравнениями (7.18) и (7.19) переходные функции имеют вид
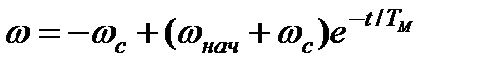 ; (7.20)
; (7.20)
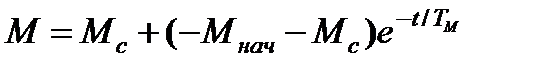 , (7.21)
, (7.21)
где 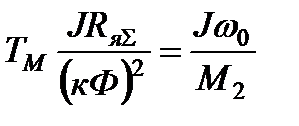 .
.
При скорости 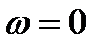 момент двигателя
момент двигателя 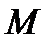 =
= 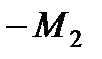 и при активном моменте, если не изменять сопротивление
и при активном моменте, если не изменять сопротивление 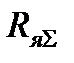 и не отключать якорь от сети, начинается разгон двигателя в обратном направлении под действием момента двигателя и активного момента
и не отключать якорь от сети, начинается разгон двигателя в обратном направлении под действием момента двигателя и активного момента 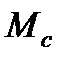 по тем же переходным функциям (7.20, 7.21) с переходом в режим рекуперативного торможения при
по тем же переходным функциям (7.20, 7.21) с переходом в режим рекуперативного торможения при 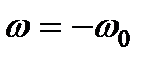 до скорости
до скорости 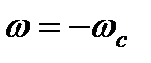 . Графики представлены на рис. 7.9,б сплошными линиями. Полное время переходного процесса при активном
. Графики представлены на рис. 7.9,б сплошными линиями. Полное время переходного процесса при активном 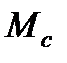
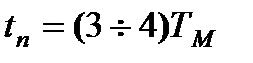 . Время же торможения проивовключением одинаково и для активного и реактивного
. Время же торможения проивовключением одинаково и для активного и реактивного 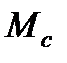 . При
. При 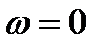 Момент двигателя
Момент двигателя 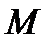 =
= 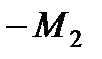 и время торможения определится из уравнения
и время торможения определится из уравнения
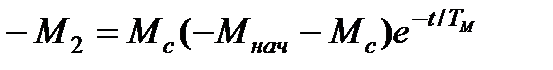 ,
,
откуда
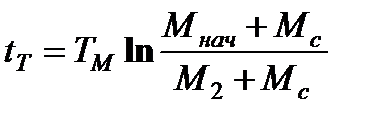 .
.
Если двигатель при реактивном 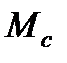 не отключать от сети линейным контактором Л, то возможны два случая:
не отключать от сети линейным контактором Л, то возможны два случая:
а) пуск двигателя с момента времени 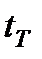 в обратном направлении без изменения
в обратном направлении без изменения 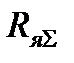 . Знак
. Знак 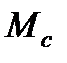 меняется на противоположный, который теперь препятствует разгону, а переходные функции будут иметь вид
меняется на противоположный, который теперь препятствует разгону, а переходные функции будут иметь вид
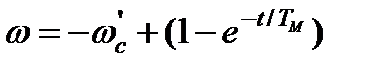 ; (7.22)
; (7.22)
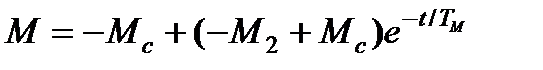 , (7.23)
, (7.23)
по которым рассчитаны зависимости 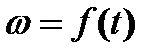 ,
, 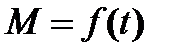 , на рис. 7.8,б они представлены штриховыми линиями. Время разгона в обратном направлении
, на рис. 7.8,б они представлены штриховыми линиями. Время разгона в обратном направлении 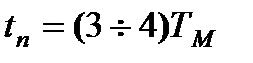 .
.
Реостатный пуск двигателя в две ступени до установившейся скорости 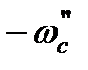 ; механические характеристики показаны на рис. 7.9,а.
; механические характеристики показаны на рис. 7.9,а.
Пример 3. Динамическое торможение
При динамическом торможении двигателя постоянного тока с независимым возбуждением якорь отключается от сети линейным контактором Л и с помощью контакта тормозного контактора Т замыкается на сопротивление динамического торможения 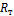 ( см. рис. 7.6).
( см. рис. 7.6).
Величина сопротивления тормозного резистора может быть определена по заданному значению максимального тормозного тока
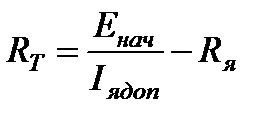 ,
,
где 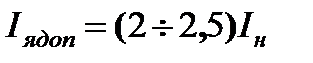 .
.
На рис. 7.10 представлены механические (скоростные) характеристики и графики переходных процессов.
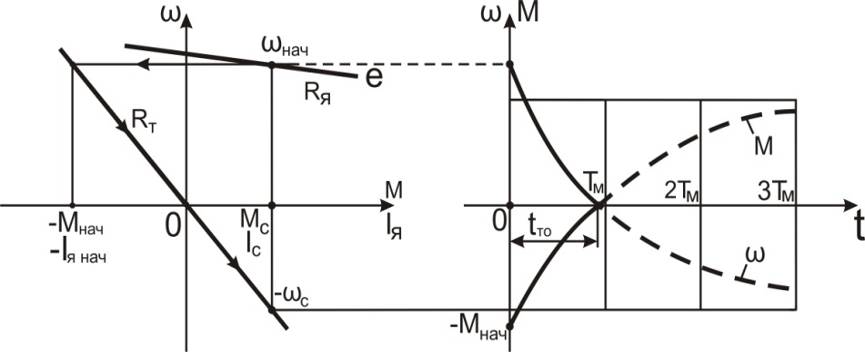
Рис. 7.10. Механические характеристики и переходные процессы при динамическом торможении
Переходные функции 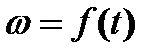 ,
, 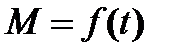 могут быть получены из уравнений (7.18) и (7.19) при изменении скорости от
могут быть получены из уравнений (7.18) и (7.19) при изменении скорости от 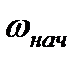 до
до 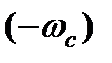 , а момента – от (
, а момента – от ( 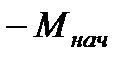 ) до
) до 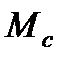 в следующем виде
в следующем виде
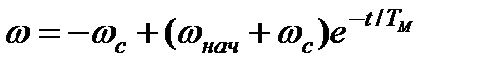 ; (7.24)
; (7.24)
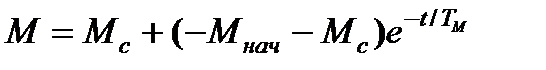 . (7.25)
. (7.25)
Время торможения до 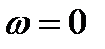
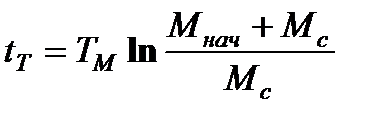 .
.
При активном моменте 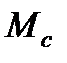 переходный процесс при
переходный процесс при 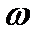 <0 продолжается уже под действием активного момента
<0 продолжается уже под действием активного момента 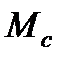 , время переходного процесса составит
, время переходного процесса составит 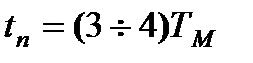 ; при
; при 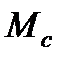 реактивном – процесс торможения заканчивается при
реактивном – процесс торможения заканчивается при 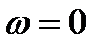 .
.
Дата добавления: 2019-02-08; просмотров: 2082;











