Политропные процессы

Условились всякий процесс идеального газа, в котором теплоем­кость является постоянной величиной, называть политропным про­цессом, а линию процесса — политропой.

Из определения политропного процесса следует, что основные тер­модинамические процессы — изохорный, изобарный, изотермический и адиабатный, если они протекают при постоянной теплоемкости, яв­ляются частными случаями политропного процесса.

Теплоемкость политропного процесса с_n может принимать самые разнообразные положительные и отрицательные значения от + ∞ до - ∞.

В результате преобразования аналитических выражений первого закона термодинамики получаем выражение:

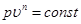. (6.21)

Полученное уравнение является уравнением политропного про­цесса.

Величина n в уравнении (6.21) называется показателем политропы; он равен

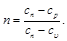(6.22)

Показатель политропы n принимает для каждого процесса опре­деленное числовое значение. Для основных процессов: изохорных n=±∞, изобарных n = 0, изотермных n = 1 и адиабатных n = k.

Поскольку уравнение политропы отличается от уравнения адиа­баты только величиной показателя n, то, очевидно, все соотношения между основными параметрами могут быть представлены формулами, аналогичными адиабатному процессу:

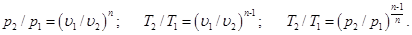
Теплоемкость политропного процесса определяем из формулы

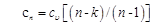. (6.23)

Уравнение (6.23) позволяет определить теплоемкость политропного процесса для каждого значения n.

Если в уравнение (6.23) подставить значения n для частных слу­чаев, то получаем теплоемкости рассмотренных процессов:

изохорного процесса n=±∞, c_n=с_υ;

изобарного процесса n=0, c_n=kс_υ=c_p;

изотермного процесса n=1, c_n=±∞;

адиабатного процесса n=k, c_n=0.

Уравнение работы изменения объема, совершаемой телом при политропном процессе, имеет аналогичный вид с уравнением работы в ади­абатном процессе, т. е.

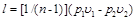, (6.24)

или

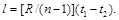(6.25)

Изменение внутренней энергии газа и теплота в политропном про­цессе определяются по формулам:

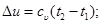
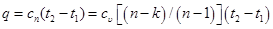. (6.26)

Изменение энтальпии в политропном процессе

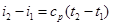. (6.27)

Изменение энтропии газа в политропном процессе определяется по формуле

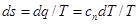, (6.30)

или для конечного изменения состояния

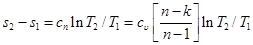. (6.31)