Основные определения

Первый закон термодинамики устанавливает взаимосвязь между количеством теплоты, изменением внутренней энергии и внешней ра­ботой газа, причем количество теплоты, подводимое к телу или отво­димое от него, зависит от характера процесса.

К основным процессам, имеющим большое значение, как для теоре­тических исследований, так и для практических работ в технике, от­носятся: изохорный, протекающий при постоянном объеме; изобарный, протекающий при постоянном давлении; изотермный, протекающий при постоянной температуре; адиабатный, протекающий при отсут­ствии теплообмена с внешней средой.

Кроме того, существует группа процессов, являющихся при опре­деленных условиях обобщающими для основных процессов. Эти про­цессы называются политропными и характеризуются постоянством теплоемкости в процессе.

Изохорный процесс

Процесс, протекающий при постоянном объеме, называют изохорным (dυ = 0, или υ = const ). Кривая процесса называется изохорой. На рис. 6.1 представлен график процесса.

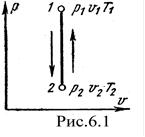Согласно закону Шарля, при постоянном объеме давление газа изменяется прямо пропорционально абсолютным температурам:

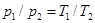. (6.1)

Внешняя работа газа при υ=const равна нулю, так как dυ = 0, т.е. l=0.

Основное уравнение первого закона термодинамики (4.6) при dl = 0 принимает вид

dq_υ = du_υ = c_υdt.

Количество теплоты, участвующее в процессе при постоянной теп­лоемкости, равно

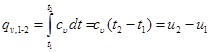. (6.2)

Вся внешняя теплота расходуется только на изменение внутренней энергии тела.

Если процесс 1-2, осуществляется с увеличением давления, теплота в нём подводится, при этом увеличивается внутренняя энергия и температура. Если давление газа в процессе понижается, то теплота отводится, уменьшается внутренняя энергия и температура (рис.6.1)

Изменение энтропии в изохорном процессе определяем из уравнения (5.21):

,

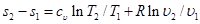но при υ=const ln υ₂/υ₁=0, поэтому изменение энтропии при посто­янной теплоемкости равно

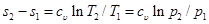. (6.3)

Как видно из данного уравнения, изохора на Тs-диаграмме пред­ставляет собой логарифмическую кривую.

Изобарный процесс

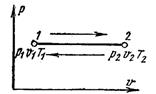
Рис. 6.2

Процесс, протекающий при постоянном давлении, называют изо­барным (dр = 0, или р = const ). Кривая процесса называется изо­барой. На рис. 6.2 изображен график про­цесса.

Из уравнения состояния идеального га­за для изобарного процесса находим

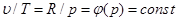
В соответствии с законом Гей-Люссака, в изобарном процессе объемы одного и того же количества газа изменяются прямо пропорционально абсолютным температурам:

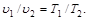(6.4)

При расширении газа его температура возрастает, при сжатии — уменьшается.

Удельная работа изменения объема при этом выражается следую­щим уравнением:

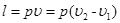, (6.5)

или

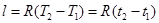. (6.6)

Основное уравнение первого закона термодинамики при р=const (dр=0) имеет вид

.

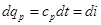Следовательно, количество теплоты, сообщенное телу в изобарном процессе при постоянной теплоемкости, равно

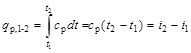; (6.7)

при переменной теплоемкости

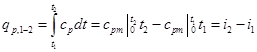. (6.8)

Для обратимого изобарного процесса при постоянной теплоемкости изменение энтропии находится по уравнению (5.23):

,

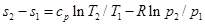но при р = const lnp₂/p₁=0, поэтому

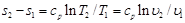. (6.9)

Изобара на Тs-диаграмме также, как и изохора, изображается логарифмической кривой.

Площадь под изобарой в некотором масштабе изображает коли­чество теплоты q_р, сообщаемое газу, равное изменению энтальпии i₂-i₁.

Из сопоставления уравнений (6.3) и (6.9) следует, что в случае осу­ществления изохорного и изобарного процессов в одном интервале тем­ператур возрастание энтропии будет больше в изобарном процессе, так как с_р всегда больше с_υ. Изобары являются более пологими кри­выми, чем изохоры (см. рис. 6.3).

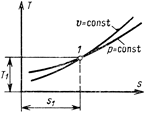
Рис. 6.3

Изотермный процесс

Процесс, протекающий при постоянной температуре, называют изотермным (Т = const, или dТ = 0). Кривая процесса называется изотермой (рис. 6.4).

Для изотермного процесса 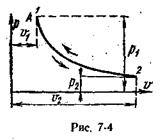объем газа изменяется обратно про­порционально его давлению (закон Бойля — Мариотта):

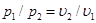. (6.10)

На рυ-диаграмме изотермный процесс представляет собой равнобокую гиперболу.

Рис. 6.4

Основное уравнение первого закона термодинамики при Т = const получает простой вид:

dq=dl и q_1-2=l_1-2.

Количество подведенной к идеальному газу теплоты численно равно работе изменения объема.

Зная уравнение изотермного процесса для идеального газа, и применяя уравнение состояния, определим удельную работу газа.

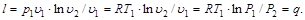(6.11)

Энтальпия и внутренняя энергия идеального газа не меняются,
т. е. di =0 и du = 0.

Изотермный процесс на Ts-диаграмме изображается горизонтальной прямой, параллельной оси абсцисс. Для определения изменения энтропии следует воспользоваться уравнениями (5.21) и (5.23) при T=const, после чего плучаем:

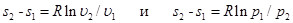. (6.12)

Теплота, участвующая в изотермном процессе, равна произведению изменения энтропии (s₂ – s₁) на абсолютную температуру Т:

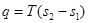. (6.13)

Адиабатный процесс

Процесс, протекающий без подвода и отвода теплоты, т. е. при от­сутствии теплообмена рабочего тела с окружающей средой, называют адиабатным, а кривая этого процесса называется адиабатой. Для по­лучения адиабатного процесса необходимым и обязательным усло­вием является dq = 0 и, следовательно, q= 0.

Обратимый адиабатный процесс можно осуществить в цилиндре с абсолютно нетеплопроводными стенками при бесконечно медленном перемещении поршня.

Уравнение адиабаты выводится на основе уравнения первого закона термодинамики и имеет вид:

pυ^k=const. (6.14)

При адиабатном процессе произведение давления на объем газа в степени k есть величина постоянная. Величину k называют показателем адиабаты. Показатель адиабаты k=c_p/c_υ (см. раздел5.5).

В соответствии с уравнением (6.14) адиабата в pυ – диаграмме графически изображена неравнобокой гиперболой АВ (см. рис. 6.5, а).

Рассмотрим зависимость между основными параметрами в адиабатном процессе.

Из уравнения адиабаты следует, что

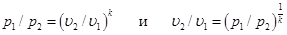. (6.15)

Зависимость между температурой, объёмом и давлением газа в процессе выражается соотношением:

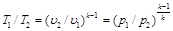. (6.16)

Уравнение первого закона термодинамики для адиабатного процесса принимает вид:

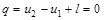
или

l = u₁ – u₂. (6.17)

Это значит, что работа изменения объема в адиабатном процессе получается за счет убыли внутренней энергии тела;

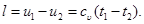(6.18)

Если газ расширяется, то его внутренняя энергия и температура убывают; если газ сжимается, то его внутренняя энергия и темпера­тура возрастают.

Работу газа также можно определить из следующих соотношений:

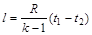(6.19)

или

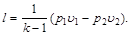(6.20)

Графически внешняя работа изображается на рυ-диаграмме пл. 12v₂v₁ (рис. 6.5, а).

Из рис. 6.5 видно, что поскольку в уравнении адиабаты k > 1, она на рυ-диаграмме идет круче, чем изотерма.

Для обратимого адиабатного процесса dq =0, поэтому

ds = dq/T = 0 и s₂-s₁ = const,

т. е. обратимый адиабатный процесс является одновременно изоэнтропным (или при постоянной энтропии) и изображается в Тs-диаграмме вертикальной прямой 1 – 2, параллельной оси ординат (см. рис. 6.5, б).

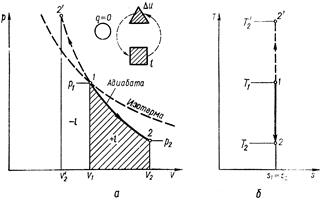
Рис. 6.5