Универсальное уравнение состояния идеального газа
Уравнению Клапейрона можно придать универсальную форму, если газовую постоянную отнести не к 1 кг газа, а к 1 кмоль.
Согласно закону Авогадро при одинаковых температурах и давлениях в равных объемах различных идеальных газов содержится одинаковое количество молекул. Из закона Авогадро вытекает, что плотности газов, находящихся при одинаковых температурах и давлениях, прямо пропорциональны их молекулярным массам:
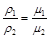 , (2.9)
, (2.9)
где μ1; μ2 – молекулярные массы газов.
Отношение плотностей газов в уравнении (2.9) можно заменить обратным отношением удельных объемов. Тогда
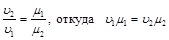 .
.
Это соотношение показывает, что при одинаковых физических условиях произведение удельного объема газа на его молекулярную массу есть величина постоянная и не зависит от природы газа:
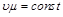 . (2.10)
. (2.10)
Произведение 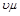 =Vμ есть объем 1 кмоль идеального газа, т.е. такого количества газа масса которого выраженная в кг, численно равна его молекулярной массе. Уравнение (2.10) показывает, что объемы киломолей всех газов при равных температурах и давлениях одинаковы.
=Vμ есть объем 1 кмоль идеального газа, т.е. такого количества газа масса которого выраженная в кг, численно равна его молекулярной массе. Уравнение (2.10) показывает, что объемы киломолей всех газов при равных температурах и давлениях одинаковы.
Напишем уравнение состояния для 1 кмоль газа:
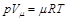 , (2.11)
, (2.11)
откуда
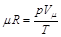 .
.
Произведение 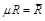 называют универсальной газовой постоянной.
называют универсальной газовой постоянной.
При так называемых нормальных физических условиях (давлении 101325 н/м2 и температуре 273,15° К) объем 1 кмоль газа равен 22,4143 м3/кмоль, а универсальная газовая постоянная оказывается равной
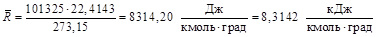 .
.
Из уравнения (2.11) получаем уравнение состояния Клапейрона – Менделеева:
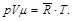 (2.12)
(2.12)
Зная универсальную газовую постоянную μR, можно подсчитать известную уже нам величину R:
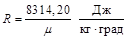 .
.
газов.
Газовая смесь может быть задана массовыми, объемными и мольными долями.
Массовой долей называется отношение массы каждого газа к общей массе смеси:
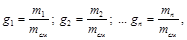 (3.2)
(3.2)
где 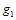 ,
, 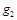 , …
, … 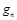 – массовые доли; m1 m2, ..., mn – масса каждого газа;
– массовые доли; m1 m2, ..., mn – масса каждого газа;
mсм – масса всей смеси.
Сумма массовых долей равна единице:
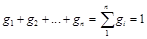 .
.
Объемной долей называется отношение парциального (приведенного) объема каждого газа к общему объему смеси газов:
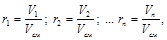 (3.3)
(3.3)
где r1, r2, ... rn – объемные доли; V1 V2, ... Vn – парциальные (приведенные) объемы каждого газа; Vсм – объем смеси газов.
Парциальным объемом газа называется объем, который занимал бы этот газ, если бы его температура и давление равнялись температуре и давлению смеси газов.
Общий объём смеси газов равен
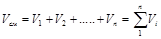 . (3.4)
. (3.4)
Сумма парциальных объемов газов, составляющих смесь, равна объему смеси газов.
Сумма объемных долей равна единице:
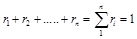 .
.
Задание смеси мольными долями равнозначно заданию её объемными долями.
Между удельными объемами, плотностями, молекулярными массами и газовыми постоянными какого-нибудь газа и всей смеси в целом на основании закона Авогадро и уравнения Клапейрона – Менделеева существует следующая зависимость:
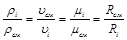 , (3.5)
, (3.5)
где 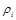 – плотность каждого газа;
– плотность каждого газа; 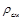 – плотность смеси газов;
– плотность смеси газов; 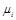 – молекулярная масса каждого газа;
– молекулярная масса каждого газа; 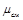 – молекулярная масса смеси газов.
– молекулярная масса смеси газов.
Можно записать также, что
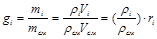 . (3.6)
. (3.6)
Последнее соотношение позволяет составить несколько уравнений, для расчёта параметров газовой смеси.
Для перевода массовых долей в объемные пользуются формулой
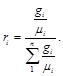 (3.7)
(3.7)
Объемные доли переводят в массовые по формуле
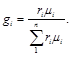 (3.8)
(3.8)
Плотность смеси ρсм, кг/м3, определяют из выражения
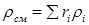 (3.9)
(3.9)
или, если известен массовый состав, по формуле
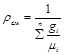 . (3.10)
. (3.10)
Удельный объем смеси представляет величину, обратную ρсм; поэтому, если дан объемный состав смеси, то
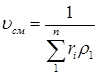 (3.11)
(3.11)
Если же известен массовый состав, то
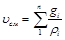 . (3.12)
. (3.12)
Из уравнения (3.9) легко получить значение так называемой кажущейся молекулярной массы газовой смеси
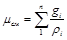 (3.13)
(3.13)
или через массовый состав
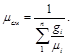 (3.14)
(3.14)
Газовую постоянную смеси газов (Rcм) можно выразить или через газовые постоянные отдельных компонентов, входящих в смесь, или через кажущуюся молекулярную массу смеси
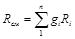 (3.15)
(3.15)
или
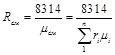 . (3.16)
. (3.16)
Парциальные давления определяются проще всего, если известны объёмные доли отдельных компонентов входящих в смесь;
p1 = pсмr1, p2 = pсмr2 и т.д.
или вообще
pi = Рсм ∙ ri, (3.17)
где pi – парциальное давление любого газа, входящего в смесь.
Дата добавления: 2020-07-18; просмотров: 773;











