Визначення рівня надійності системи з паралельним з’єднанням елементів

План лекції

1. Особливості побудови системи з паралельним з’єднанням елементів.

2. Методика резервування ФЕ в системах з навантаженими і ненавантаженими резервами.

3. Аналітичні співвідношення для визначення рівня надійності систем з паралельним з’єднанням елементів.

Одним з ефективних методів підвищення надійності систем є резервування елементів цієї системи, використовуючи за рахунок паралельне з’єднання ФЕ.

Розглянемо методи розраховування характеристик надійності для систем із структурним резервуванням. За такого типу резервування визначають основні елементи, які використовуються у схемі для реалізації алгоритму функціонування, і резервні елементи, які забезпечують працездатний стан системи у випадку відмови будь-якого із основних елементів. Відношення числа резервних елементів до числа основних елементів називається кратністю резервування. Резервування, кратність якого дорівнює одиниці, називається дублюванням.

Резерв може бути відновлювальним і невідновлювальним залежно від того, відновлюється чи не відновлюється резервний елемент після того, як він відмовив.

Основні елементи у сукупності з резервними елементами створюють паралельне об’єднання елементів. Відмова системи наступає у тому випадку, коли відмовляють як всі основні, так і всі резервні елементи.

Якщо резервування не передбачає відновлення, тобто система працює до першої відмови, а при цьому відмови незалежні, то імовірність P(t) безвідмовної роботи системи протягом певного часу t визначається залежністю

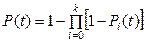, (24.1)

де 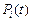– імовірність безвідмовної роботи і-го елементу за час t.

Якщо значення імовірністей 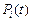елементів рівні між собою, з урахуванням того, що P_i(t) = P₁(t), то можна записати:

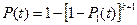, (24.2)

де k – кількість резервних елементів.

У процесі проектування ЕА розробниками вирішується завдання визначення кількісних співвідношень значення інтенсивності відмов системи за навантаженим і ненавантаженим резервами. Визначимо суттєві особливості цього завдання.

Маємо систему з навантаженим резервом і з кількістю резервних елементів k. Якщо всі елементи мають експоненціальний закон розподілу відмов, то 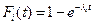. Згідно з цим:

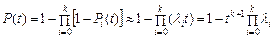. (24.3)

Якщо позначимо 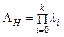– інтенсивність відмов системи з навантаженим резервом, то значення опосередкованого часу роботи такої системи можна вирахувати так:

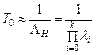. (24.4)

Розглянемо іншу систему, яка складається із k резервних ФЕ, працюють в навантаженому режимі. Передбачаємо, що відмови елементів незалежні і характеристика імовірності відмов кожного із елементів має експоненціальний закон: 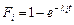. В цій ситуації:

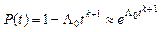, (24.5)

де 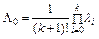– інтенсивність відмов системи з навантаженим резервом.

Порівнюючи співвідношення (4) і (3), можна зробити висновок про переваги в експлуатації ненавантаженого резерву перед навантаженим. Якщо припустити, що в зазначених системах однакова кількість елементів з рівним значенням інтенсивності відмов, тоді неважко побачити, що 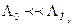. Отже:

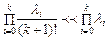, (24.6)

З практичного боку, кожна система у своїй структурі має певну кількість перемикачів. Тому, розглянемо, як розрахувати надійність системи з перемикачем для двох варіантів: перемикач послідовно вмикає всі резервні елементи і кожний із резервних елементів має свій перемикач.

Для першого варіанта будемо передбачати: задано імовірності безвідмовної роботи елементів як основного P₀(t), так і резервного і-го елементу P_і(t), а також імовірність перемикача P_П(t). Для визначення імовірності безвідмовної роботи системи з перемикачем можна використати формулу повної імовірності. Позначимо: P(t) = P; P₀(t) = P₀ і P_і(t) = P_і.

Тоді

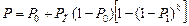. (24.7)

Із формули (24.7) випливає, що відмови усіх елементів мають незалежний характер.

Розглядаючи другий варіант підключення перемикача, передбачаємо, що відмови перемикачів і елементів відбуваються незалежно. Умовно система розбивається на підсистеми, які складаються з послідовно з’єднаних резервних елементів і перемикача (одного або більше). Надійність кожної із таких підсистем позначимо P′_і, надійність перемикача P_Пі і надійність резервних елементів P_і. Враховуючи позначення 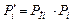і використовуючи формулу повної імовірності, зазначаємо, що рівень надійності зазначеної системи може бути розрахований:

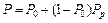, (24.8)

де P_p – надійність резерва із k елементів, .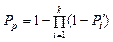

З урахуванням отриманого:

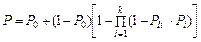. (24.9)

Якщо надійність усіх резервних елементів позначити як 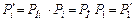, то рівняння (9) спрощується

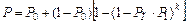. (24.10)

Визначимо особливості резервування. Якщо в системі резервуються окремі елементи або їх групи, то таке резервування називається роздільним. Якщо об’єкт резервується у цілому, то такий вид резервування називається загальним резервуванням.

Але, як свідчить досвід експлуатації, збільшення масштабу резервування призводить до зменшення рівня надійності всієї системи.

Контрольні питання

1. Назвіть, які основні характеристики систем з паралельним з’єднанням елементів?

2. Поясніть, в чому полягає сутність резервування ФЕ в системах ЕА?

3. Розкажіть, які існують порівняльні ознаки відновлюваних і невідновлюваних систем з паралельним з’єднанням ФЕ?

Література – [6].

Список літератури

1. Кузовик В. Д. Надійність пілотажно-навігаційних комплексів : (конспект лекцій) / Кузовик В. Д. – К. : НАУ, 2004. – 78 с.

2. Дедков В. К., Основные вопросы эксплуатации сложных систем. / Дедков В. К., Северцев Н. А. – М. : Высш. школа, 2000. – 430 с.

3. Барзилович Е. Ю. Модели технического обслуживания сложных систем. / Барзилович Е. Ю. – М. : Высш. школа, 1998. – 231 с.

4. Евланов Л. Г. Контроль динамічних систем. / Евланов Л. Г – М. : Наука, 1997. – 424 с.

5. Котов В. Е. Сети Петри. / Котов В. Е. – М. : Наука, 1994. – 159 с.

6. Синдеев И. М. Диагностика сложных объектов. / Синдеев И. М. – М. : Наука, 1980. – 126 с.

7. Краус М. Сбор данных в управляющих вычислительных системах. / Краус М., Кубчах Э. – М. : Мир, 2002. – 294 с.

8. ДСТУ 2860-94 "Надійність техніки. Терміни та визначення". Чинний від 01.01.1996. – К. : Держстандарт України, 1995. – 92 с.