Критерії оптимізації безумовних програм оцінки технічного стану

План лекції

1. Загальна характеристика критерію оптимізації.

2. Методика побудови програми оцінки технічного стану програми діагностування.

3. Приклад застосування методу гілок і меж для побудови оптимальної програми діагностування.

Із досвіду експлуатації встановлено, що раціональним критерієм оптимізації програми оцінки технічного стану є економічний показник, а саме рівень собівартості реалізації операцій або контролю працездатності, або діагностування можливих відмов. Вартість проведення зазначених процедур оцінки технічного стану залежить від ряду факторів, серед яких такі, як рівень контроле- і ремонтопридатності об’єкта оцінки технічного стану, а також рівень імовірності знаходження об’єкта в тому стані, який визначається відмовами того чи іншого елемента.

На практиці для отримання оптимальної програми оцінки технічного стану електронної апаратури застосовується метод гілок та границь. Розглянемо процес реалізації зазначеного методу на прикладі системи, яка складається із п’яти блоків функціонально-логічної моделі і для якої побудована матриця станів (табл. 18.1)

Таблиця 18.1

Матриця станів

S	P(S)	П
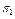
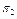
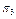
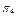
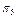
S1	0.2
S2	0.05
S3	0.24
S4	0.15
S5	0.06
S6	0.3
C*н	----	23.4	5.32	20.72	18.2	12.5

В табл. 18.1 під 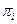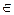П представлено 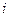-а перевірка, яка реалізує процес контролю значень вхідних і вихідних параметрів блоку із функціонально-логічної моделі. Сукупність етапів системи S складається із шести рівнів. Так, S₁ – відповідає стану системи у випадку відмови блока 1; S₂ – відповідає стану системи у випадку відмови блока 2. Аналогічно процедура побудови сукупності {S} матриці станів стосується {S₃; S₄; S₅}. Кортеж одиниць стану S₆ характеризує повну працездатність усіх п’яти блоків системи. Інформація в матриці станів, яка представлена показником P(S), визначає кількісні значення імовірностей появи одного із шести станів системи залежно від стану працездатності одного із блоків системи. Передбачається, що у будь-який проміжок часу в системі можлива тільки ординарна відмова (може відмовити одночасно тільки один блок системи).

Таким чином, сутність процесу виконання програми оцінки технічного стану можна охарактеризувати так. Для системи S визначено сукупність перевірок 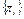з метою локалізації (діагностування) одиничної відмови, яка визначає працездатний стан системи із значенням імовірності P(S). Пошук відмови на основі безумовної програми оцінки технічного стану можна розпочати з будь-якої із п’яти перевірок. Але з практичної точки зору доцільно визначити собівартість операцій (C_H) щодо реалізації необхідної і достатньої сукупності 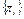перевірок. Для застосування методу гілок і границь визначаються значення бінарних імовірностей для множини {S}. Позначимо через {P^*_α} значення бінарних імовірностей для сукупності станів S_j, для яких у табл. 18.1 результат перевірки 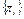відповідає 0, а через (Р^*_β) – значення сукупності станів S_i, результат перевірок яких 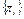відповідає 1.

Розрахунки значень середньої вартості процесу діагностування виконується за формулою:

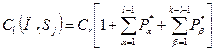, (18.1)

де 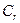– вартісний показник процесу діагностування залежно від рівня контролепридатності блока; [l, k] – кількість відповідно нульових і одиничних значень перевірок у сукупності станів .

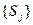Визначимо послідовно значення 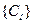для програми діагностування, починаючи з умовної реалізації перевірки 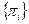, яка виділяє дві підмножини 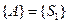і .

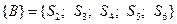Оскільки, враховуючи (18.1), значення P^*_α = 0, то упорядкуємо значення P(S) із табл. 18.1 за зростаючою послідовністю, а саме: P(S₂) = 0.05 → P(S₅) = 0.06 → P(S₄) = 0.15 → P(S₅) = 0.24 → P(S₆) = =0.3. Тоді для значення Р^*_β розраховуються значення бінарних імовірностей і будується ряд бінарних імовірностей: P^*₁ = P(S₂) + +P(S₅) = 0.11; P^*₂ = P^*₁ + P(S₄) = 0.26; P^*₃ = P^*₂ + P(S₃) = 0.5; P^*₄ = = P^*₃ +P(S₆) = 0.8. Процедуру побудови зазначеного ряду викладено в матеріалах лекції 17.

Зрештою використовуючи формулу (18.1), маємо:

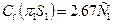(18.2)

Наступний етап розрахунків полягає в тому, що процес діагностування починається з перевірки 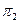. Тоді 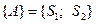; 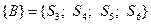. Враховуючи зазначену методику розрахунку, для визначення значення С_н( 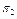;С₂) маємо таку процедуру. Представляється ряд бінарних імовірностей: P₁* = = P(S₅) + P(S₄) = 0.21; P₂* = P₁* + P(S₃) = 0.45; P₃* = P₂* + P(S₆) = = 0.75.

Використовуючи рівняння (18.1), отримуємо:

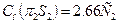(18.3)

Проведемо розрахунок, враховуючи, що програма діагностування розпочинається з перевірки 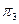. Відповідно до інформації, яку викладено в табл. 18.1, перевірка 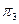диференціює всю сукупність станів {S₁ 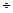S₆} на дві підмножини {A} = {S₃} і {B} = {S₁; S₂; S₄; S₅; S₆}. Тоді P(S₃) = 0.24, а враховуючи залежність (18.1), значення для P_α* = 0. Для розрахунку значень бінарних ймовірностей підмножина {B} упорядковується так: P(S₂) = 0,05 → → P(S₅)= 0,06 → P(S₄) = 0,15; P(S₁) = 0,2 → P(S₆) = 0,3.

Відповідно до рівняння (18.1), значення бінарних ймовірностей для підмножини {B} будуть так: P₁* = P(S₂) + P(S₅) = 0.11; P₂* = = P₁* + P(S₄) = 0.26; P₃* = P₂* + P(S₁) = 0.46; P₄* = P₃* + P(S₆) = 0.76. В результаті: P_β* = 1.59.

Виходячи із викладеного, значення середньої вартості програми діагностування, яка починається з перевірки { 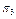}, буде складати:

C_н( 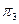;S₃) = 2.59C₃ (18.4)

За аналогічною методикою розраховуються значення для C_н( 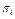; S_j) в програмі діагностування, якщо на початковому етапі реалізуються перевірки { 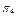} або{ }.

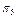Для програми діагностування, що починається з перевірки { 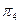} формуються дві підмножини {A} = {S₁; S₂; S₃; S₄} та {B} = {S₅; S₆}.

Утворюємо впорядковані за зростанням кортежі імовірностей для {A}: P(S₂) = 0.05 → P(S₄) = 0.15 → P(S₁) = 0.2 → P(S₃) = 0.24, для {B}: P(S₅) = 0.06 → P(S₆) = 0.3.

Тоді розраховуються значення бінарних ймовірностей: ∑P_a* = = 0.64; ∑P_β* = 0.36. В результаті:

C_н( 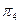;S₄) = 2.0C₄ (18.5)

Для програми діагностування, що починається з перевірки {П₅} отримуємо {A}={S₁;S₂;S₅}; {B}={S₃;S₄;S₆}. Відповідно значення бінарних імовірностей ∑P_a*=0.31; ∑P_β*=0.69. В решті:

C_ср( 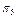;S₅)=2.0C₅ (18.6)

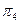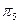Порівнюючи значення із формул (2); (3); (4); (5); (6), можна зробити попередній висновок. Якщо враховувати значення бінарних імовірностей, то програма (гілка) діагностування може бути представлена у такий спосіб. Оскільки для перевірок і значення С_н( 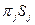) однакові, то початок програми може бути або з перевірки 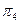, або з перевірки 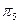, потім реалізується послідовність перевірок 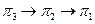. Однак, програма може суттєво змінитися, якщо враховувати собівартість операцій {C_R} діагностування, значення яких залежить від рівня контролепридатності цих блоків. Для прикладу введемо значення мінімальних витрат: C₁ = 9; C₂ = 2; C₃ = 8; C₄ = 7; C₅ = 5. Тоді: C_н*( 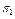;S₁) = 24.03; C_н*( 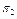;S₂) = 5.32; C_н*( 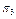;S₃) = 20.72; C_н*( 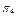;S₄) = 14.0; C_н*( 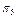;S₅) = 10.0. Очевидно, що в такій ситуації доцільно починати програму діагностування з перевірки { 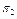} і закінчувати перевіркою { 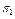}. Таким чином, і в цьому випадку можна визначити як гілки так і границі безумовної програми оцінки технічного стану блоків і модулів ЕА. Задаючи значення максимальних витрат на роботи з діагностування, можна аналогічно розрахувати верхню границю 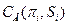, і побудувати програму діагностування.

Контрольні питання

1. Наведіть, які критерії оптимізації застосовуються для отримання ефективної програми діагностування?

2. Поясніть, в чому полягають етапи побудови ряду бінарних ймовірностей?

3. Розкажіть, які значення має рівень контролепридатності для діагностування об’єкта контролю?

Література: [6]; [7].