Застосування характеристик надійності відновлюваних модулів електронного обладнання в технологіях оцінки технічного стану

План лекції

1. Класифікаційний аналіз стаціонарних і нестаціонарних потоків відмов ФЕ.

2. Аналітичні співвідношення для розрахунків характеристик надійності.

3. Методика побудови ефективного процесу оцінки ТС модулів ЕА.

Оскільки відмови, які виникають в модулях ЕА, є випадковими подіями, то час роботи 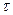технічного приладу до моменту відмови також є випадковою величиною. Послідовність подій, які виникають одна за одною у випадкові проміжки часу, називають потоком подій.Потік подій має назву ординарного, якщо імовірність попадання на який завгодно інтервал часу 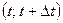двох (і більше) подій безмежно мала порівняно з імовірністю попадання однієї події.

Потік подій називається потоком без наслідків, якщо імовірність попадання 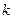подій на інтервал 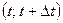не залежить від кількості і моментів появи подій на інших ділянках, які не перетинаються з попередніми. Ординарний без наслідків потік називається пуассонівським. Якщо процес подій створює пуассонівський потік, то множина подій, які потрапляють на будь-яку ділянку в часі 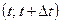, розподілена за законом Пуассона. При цьому імовірність того, що випадкова величина 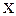потрапить на інтервал 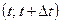, дорівнює

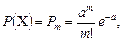
де 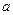– параметр закону Пуассона:

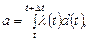
де 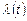– інтенсивність потоку відмов.

Якщо імовірність попадання 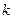подій на інтервалі 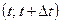залежить від числа 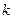та довжини інтервалу 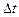і не залежить від положення інтервалу 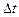, то такий потік називається стаціонарним. Для стаціонарного потоку інтенсивність постійна і величина математичного очікування незмінна.

Потік, що має властивості ординарності та стаціонарності за відсутності наслідків, називається простішим. Для простішого потоку кількість подій, які потрапляють на довільний інтервал часу довжиною 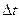, розподілена за законом Пуассона, з параметром

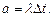
Час 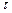між двома сусідніми подіями в простішому потоці є випадковою величиною, яка має експоненціальний закон розподілу із щільністю:

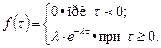
Розглянемо характеристики надійності невідновлюваного модуля, працездатного в початковий момент роботи 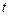= 0 і працюючого до першої відмови, яка виникає у випадковий момент 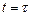. Надійність такого модуля повністю визначається його безвідмовністю – часом працездатного стану модуля. Позначимо щільність імовірності відмови

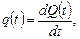(21.1)

де 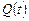- імовірність відмови (функція розподілу ).

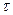Тоді імовірність безвідмовної роботи модуля за час 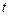можна виразити:

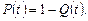(22.2)

Очевидно кількісна величина 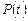змінюється в межах [0¸1]. Таким чином, надійність об`єкта є основною характеристикою працездатності.

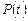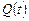Паралельно з такими характеристиками об`єкта як і , в процесі експлуатації розглядається ще одна характеристика – середній час безвідмовної роботи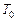

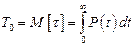
або

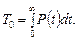
Для невідновлюваних модулів важливим показником надійності є щільність виникнення відмови, яка на практиці класифікується як інтенсивність відмови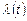

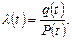(20.3)

Підставляючи в (3) формули (1) і (2), а також виконавши нескладні перетворення, отримаємо:

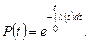(20.4)

Для більшості модулів електронного обладнання у процесі експлуатації інтенсивність відмов змінюється за законом, який має три характерні періоди. Перший період відноситься до етапу приробки модулів, коли інтенсивність зменшується за рахунок усунення систематичних відмов ФЕ (відмови: конструктивні, виробничі, експлуатаційні). Другий період належить до етапу нормальної експлуатації модулів, коли інтенсивність відмов практично залишається незмінною.

Саме в такий період експлуатації постійним залишається і рівень безвідмовності роботи цих модулів. Третій період експлуатації характеризується старінням і зносом модулів, у зв`язку з чим інтенсивність відмов цих модулів збільшується.

Із наведених трьох періодів найбільшим за часом є другий період – період нормальної експлуатації модулів. Як уже було зазначено, протягом цього періоду інтенсивність відмов практично залишається незмінною, тобто 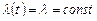. Враховуючи зазначене, із співвідношення (20.4) отримаємо

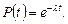(20.5)

Тоді

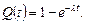(20.6)

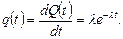(20.7)

Визначено, що випадкова величина, для якої виконуються умови (5.5), (5.6), (5.7), мають експоненційний закон розподілу. Для експоненційного закону математичне очікування вираховується так: 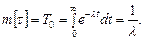Якщо дисперсія цього закону розподілу дорівнює 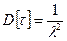; тоді, середньоквадратичне відхилення буде дорівнювати 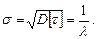Отже, для експоненційного закону розподілу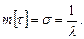

Зауважимо, що у практичних розрахунках основних характеристик експоненційного розподілу можуть бути використані залежності

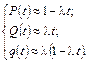(20.8)

Використовуючи систему рівнянь (20.8), похибка при розрахунках значення не перевищує 0,5 %.

Із викладеного матеріалу можна зробити суттєві для експлуатації ЕА висновки. Перш за все, для отримання ефективної технології оцінки ТС необхідно так коректно планувати експеримент, щоб одержати вірогідні значення статистичних даних про відмови ФЕ в модулях. Після того, як статистичні дані одержано, важливий етап полягає у визначенні закону розподілу відмов ФЕ як випадкових величин. Крім того, для потоку відмов необхідно визначити властивості стаціонарності (нестаціонарності). Розрахунки основних параметрів надійності необхідно проводити відповідно до визначеного закону розподілу відмов ФЕ.

Очевидно, що для будь-якого модуля ЕА, що має визначені параметри надійності, формування технології оцінки ТС необхідно починати з того модуля, у якого найнижчий рівень значень характеристик надійності ФЕ.

Контрольні питання

1. Визначити, якими властивостями характеризуються стаціонарні й нестаціонарні потоки відмов ФЕ?

2. Подати, які аналітичні вирази застосовуються при розрахунках основних характеристик надійності?

3. Охарактеризувати, в чому полягають ознаки формування технологій оцінки технічного стану модулів ЕА?

Література – [6].