Визначення рівня надійності систем з послідовним з’єднанням елементів

План лекції

1. Методика визначення рівня надійності відновлюваних систем з послідовно з’єднаними елементами.

2. Методика визначення рівня надійності невідновлюваних систем.

3. Аналітичні співвідношення для розрахунку рівня надійності систем з послідовно з’єднаними елементами.

Блоки як елементи ЕА, які реалізують в системі алгоритм функціонування, можуть бути з’єднанні між собою різним чином: послідовно, паралельно, комбіновано, а також без резервування або з резервуванням. Крім того, резервування може бути побудоване в активному або пасивному варіантах.

Розглянемо, як розраховується рівень надійності для систем з різними варіантами з’єднання елементів (блоків).

Системи з послідовним з’єднанням елементів. Структурна схема розрахунку надійності для послідовного з'єднання елементів може бути представлена так, як показано на рис. 23.1.

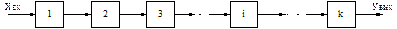
Рис. 23.1. Структура послідовно з’єднаних елементів

Виконуючи розрахунки надійності такої системи, передбачаємо, що вона має обмежену кількість елементів, а відмова одного елемента приводить до відмови всієї системи (за умови, що всі відмови елементів незалежні).

Розглянемо випадок, коли всі послідовно з’єднанні елементи системи працюють до першої відмови. Враховуючи, що відмови незалежні, запишемо

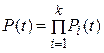, (23.1)

де 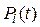– імовірність безвідмовної роботи за час t для і-го елемента.

Тоді,

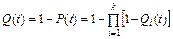. (23.2)

В практиці під час вирішення завдань, коли 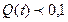використовуються такі співвідношення

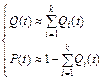. (23.3)

Якщо для елементів системи відомі інтенсивності відмов λ_і, то інтенсивність відмови всієї системи буде

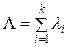. (23.4)

Якщо імовірність безвідмовної роботи всіх елементів системи має експоненціальний закон розподілу, то

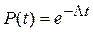. (23.5)

З урахуванням (3); (4); (5) визначимо математичне очікування системи до першої відмови або середній час роботи системи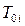

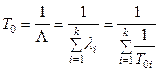, (23.6)

де 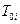– середній час роботи і-го елемента системи.

Поставимо умову, що в системі з послідовно з’єднаними елементами кожний із елементів відновлюється миттєво і в повному обсязі. Тоді випадкова величина кількості відмов такої системи {r(t)} (до моменту часу t) може бути представлена як сума незалежних випадкових величин r_i(t) кількості відмов і-го елемента до моменту t:

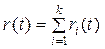. (23.7)

Враховуючи (7), інтенсивність (функція) відновлювання системи може бути представлена:

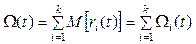, (23.8)

де 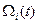– функція відновлення і-го елемента.

Якщо справедливе співвідношення (8), то з визначенням щільності відновлення аналітичний вираз буде таким:

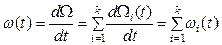, (23.9)

де 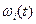– параметр потоку відмовлень (щільність відновлення) і-го елементу.

У тому випадку, коли потоки відмов усіх елементів можуть бути представлені експоненціальним законом, тоді параметр потоку відмов і-го елемента є постійним .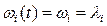

Тому щільність відновлення і параметр потоку відмов системи також будуть постійними і можуть бути представлені у такому вигляді:

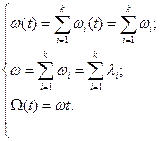(23.10)

Якщо система складається із достатньо великої кількості незалежних елементів з миттєвим і повним відновленням (при цьому інтенсивність відмов кожного із елементів в системі мала), то сумарний потік може бути представлений як пуассонівський потік без наслідків. Тоді аналітично імовірність появи рівно m відмов (відновлювань) системи за час t може бути представлена:

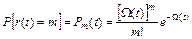. (23.11)

Згідно з цим, для невідновлюваних і відновлюваних систем розрахунки рівня надійності мають власні особливості. Ці обставини необхідно враховувати під час виконання практичних розрахунків. Також необхідно пам’ятати, що якість отриманих результатів суттєво залежить від точності оброблення статистичних даних відмови блоків ЕА.

Контрольні питання

1. Поясніть, які ознаки характеризують відновлювальні системи?

2. Поясніть, які ознаки характеризують невідновлювальні системи?

3. Охарактеризуйте, які основні параметри надійності застосовуються для аналізу системи з послідовним з’єднанням елементів?

Література – [6].