Группы пространственной симметрии

<1 2 345 6 7 >

В пространственных группах симметрии кристалла к преобразованиям, которые принадлежат к симметрии точечной группы, добавляются еще и трансляции. Группа трансляций – это перенос атомов (групп атомов вдоль любого направления на одно и то же определенное расстояние, которое называется периодом трансляции.

Произведение доли периода трансляции на операцию отражения в плоскости симметрии порождает новое симметричное превращение – плоскость скользящего отражения. Плоскость скользящего отражения, которая ориентирована в плоскости 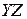, отражается символом 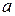, в плоскости 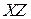– символом 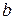, в плоскости 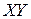– символом .

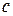Скольжение может быть направлено не только вдоль основных трансляций, а вдоль диагонали, построенной, например, на элементарных трансляциях 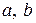. Если перенос проводится на половину длины диагонали, плоскость помечают символом 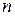, на четверть длины диагонали – символом 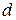, такие плоскости называют «алмазными», поскольку они характерны для кристаллов, которые имеют структуру алмаза (рис.1.9, а). Число рядом с фигуркой означает перемещение в частях периода трансляции.

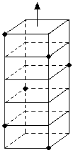
Произведение доли периода трансляции на поворот вокруг оси порождает винтовой поворот. Винтовой осью симметрии называется совокупность оси симметрии и переноса вдоль этой оси, которые действуют совместно. После этой операции симметрии исходная точка должна совместиться со второй, какая идентичная первой. Винтовые оси симметрии в кристаллических структурах могут быть только 2, 3, 4 и 6 порядков. Винтовая ось отражается цифрой с цифровым подстрочным индексом: цифра означает порядок оси, а часть от деления индекса на порядок оси показывает, на какую долю трансляции происходит перенос вдоль винтовой оси при повороте, который отвечает действия рассматриваемой оси (рис.1.5).

Все возможные кристаллические структуры описываются 230 пространственными группами симметрии. Пространственной группой симметрии называют соединение всех возможных неоконченных превращений симметрии кристаллической структуры. Пространственная группа симметрии определяет симметрию кристаллической структуры таким же образом, как точечная группа симметрии определяет симметрию внешней формы кристалла и симметрию его макроскопических свойств.

Каждой группе симметрии отвечает несколько пространственных групп. Точечную группу, которая отвечает пространственной группе симметрии, можно получить, если мысленно уничтожить все трансляции, то есть превратить плоскости скользящего отражения в простые зеркальные плоскости, винтовые оси в обычные поворотные оси симметрии и свести все оставшиеся элементы симметрии в точку.


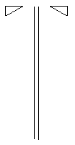
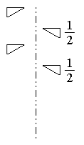
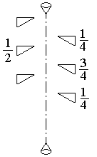
m	n	D	4₁
Рис.1.5. Плоскости зеркального отражения и винтовая ось симметрии

Вывести из точечной группы симметрии все пространственные группы, которые ей принадлежат, – более сложная задача. Впервые они были получены одновременно и независимо Е.Федоровым[4] и А.Шенфлисом. Поэтому их еще называют федоровскими.

Международная символика пространственных групп симметрии составлена таким образом, что по виду символа можно полностью представить взаимное расположение элементов симметрии (табл..1.3). Отсутствие элемента на соответствующей позиции отражается цифрой 1. Например, к точечной группе симметрии 32 принадлежат пространственные группы: Р321, Р3121, Р3221, Р312, Р3112, Р3212.

1.5. Решетки Браве[5]

Кристаллическая решетка превращается сама в себя при преобразованиях, которые отвечают точечной группе, а также при трансляциях. Полная группа преобразований, которая совмещают решетку саму с собой, называется группой Браве. Решетки, которые выводят из одной точки группой Браве, называют решетками Браве.

Симметрия кристаллического пространства налагает ограничение на количество возможных решеток. Существует всего 14 пространственных решеток (трансляционных решеток Браве), которые принадлежат 7 кристаллографическим системам симметрии (сингониям) (см. таблицу 1.1 и рис. 1.6 ).

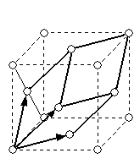
Из них 6 являются примитивными. Но каждой из не примитивных решеток соответствует примитивная ячейка. Например, ОЦК и ГЦК решетки можно заменить примитивными ромбоэдрами (рис. 1.7).

Решетка должна быть инвариантной ко всем превращениям симметрии, которые возможны для данного кристаллического пространства.

Элементарные ячейки в решетках Браве выбираются таким образом, чтобы:

– симметрия их отвечала симметрии всей решетки;

– количество прямых углов и одинаковых сторон были максимальным;

– объем ячейки был минимальным.

Таблица 1.1. Элементарные ячейки Браве

Кристаллография система Число ячеек Символ ячейки Характеристика ячейки

Триклинная P а¹b¹c; a¹b¹g¹90^o

Моноклинная Р,С а¹b¹c; a=g=90^o; b¹ 90^o

Ромбическая Р,С,I,F а¹b¹c; a=b=g=90^o

Тетрагональная P,I a=b¹c; a=b=g=90^o

Кубическая P,I,F a=b=c; a=b=g=90^o

Тригональная R a=b=c; a=b=g<120^o,¹ 90^o

Гексагональная P a=b¹c; a=b=90^o, g=120^o

Решетка

примитивная базо-центрированная объемно-центрированная гране-центрированная

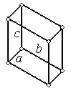
Триклинная сингония

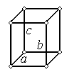
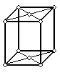
Моноклинная сингония

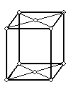
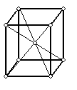
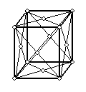
Ромбическая сингония

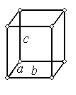
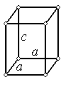
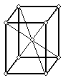
Тетрагональная сингония

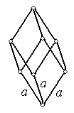
Тригональная (ромбоэдрическая) сингония

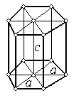
Гексагональная сингония

Кубическая сингония

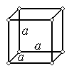
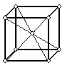
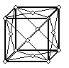
Рис.1.6. Пространственные решетки Браве

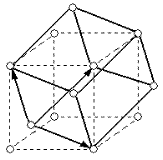
а б

Рис.1.7. Примитивные ячейки для ОЦК (а) и ГЦК (б) решеток

В пространственных группах симметрии имеем только четыре типа решеток Браве: примитивная P, объемно-центрированная I, гранецентрированная F, базоцентрированная C.

14 решетками Браве исчерпываются все возможные трансляционные решетки кристаллических структур. В структурах кристаллов решетки Браве могут быть вставлены одна в другую, а в узлах различных решеток могут находиться как одинаковые, так и неодинаковые атомы.

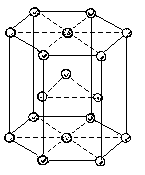
Наиболее распространенные среди металлов пространственные решетки относительно просты и совпадают с трансляционными: объемно-центрированная кубическая, гранецентрированная кубическая. Плотно упакованная гексагональная среди металлов (рис.1.8), а среди полупроводников – кубическая типа алмаза или цинковой обманки (рис.1.9) не менее широко распространены. Последние представляют удвоенную гранецентрированную кубическую.

Сама по себе пространственная решетка не определяет положения атомов в кристалле, а является геометрическим образом, который отвечает некоторому размещению точек в пространстве.

Рис.1.8. Гексагональная плотно упакованная решетка

Для описания структуры кристалла необходимо, кроме решетки, указать базис. Под базисом решетки понимают совокупность координат минимального числа частиц, выраженную в осевых единицах, трансляцией которой в трех осевых направлениях образуется данная решетка.

Если базис содержит только один атом, то решетка называется примитивной (или простой), в другом случае, если базис включает несколько атомов, говорят о решетке с базисом. Можно показать, что все решетки Браве является простыми, хотя элементарные ячейки могут содержать и более одного атома. Решетка с базисом может быть представлена как совокупность нескольких решеток Браве, вставленных одна в другую.

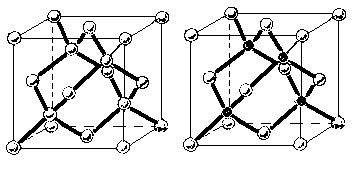
Например, решетка типа алмаза может рассматриваться в виде двух кубических гранецентрированных решеток, смещенных друг относительно друга на четверть длины пространственной диагонали ячейки (рис.1.9а).

Среди бинарных полупроводниковых соединений типа А^IIIВ^V и A^ІІB^VІраспространена решетка типа цинковой обманки ZnS (рис.1.9, б). Такая структура получается из структуры алмаза, если атомы цинка разместить в одной из гранецентрированных решеток, а атомы серы – в другой. Вокруг каждого атома на одинаковом расстоянии от него находятся четыре атома другого сорта, размещенных в углах правильного тетраэдра. Примерами таких соединений могут служить ІnSb, ІnAs, ІnP, GaAs, GaSb, GaP.

а б

Рис.1.9. Кубическая решетка типа алмаза (а) и типа цинковой обманки (б)

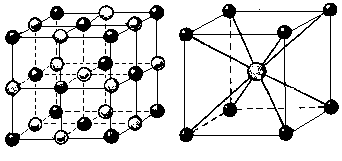
Интерес представляют также кубические структуры типа хлористого натрия и хлористого цезия (рис.1.10). Решетка Браве NaCl – кубическая гранецентрированная, базис которой состоит из двух атомов: одного атома Na и одного атома Cl, которые находятся один от другого на расстоянии, равном половине длины параметра решетки. Пространственная решетка CsCl – простая кубическая, с базисом из одного атома Cs и одного атома Cl.

а б

Рис.1.10. Кубические решетки хлористого натрия (а) и хлористого цезия (б)

Для характеристики кубических решеток используют следующие основные параметры:

координационное число – количество ближайших соседей атома;

атомный радиус – половина расстояния между ближайшими соседями;

число атомов в элементарной ячейке;

плотность упаковки – отношение объема, занятого атомами в ячейке, к объему ячейки.

В таблице 1.2 приведенные характеристики кубических решеток.

Таблица 1.2. Характеристики кубических решеток

Параметры Тип решетки

Прими- тивная ОЦК ГЦК Типа алмаза

Координационное число

Атомный радиус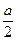

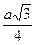
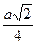
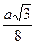
Число атомов в элементарной ячейке

Коэффициент упаковки η (плотность упаковки), %

<1 2 345 6 7 >

Дата добавления: 2020-07-18; просмотров: 622;

Поиск по сайту

Узнать еще

Публикации по технике и механике

Публикации по биологии

Публикации по информатике

Публикации по строительству

Публикации по физике

Публикации по химии

Публикации по электронике

Публикации по искусству

Публикации по истории

Публикации по медицине

Публикации по педагогике

Разделы публикаций

Кристаллография система	Число ячеек	Символ ячейки	Характеристика ячейки
Триклинная		P	а¹b¹c; a¹b¹g¹90^o
Моноклинная		Р,С	а¹b¹c; a=g=90^o; b¹ 90^o
Ромбическая		Р,С,I,F	а¹b¹c; a=b=g=90^o
Тетрагональная		P,I	a=b¹c; a=b=g=90^o
Кубическая		P,I,F	a=b=c; a=b=g=90^o
Тригональная		R	a=b=c; a=b=g<120^o,¹ 90^o
Гексагональная		P	a=b¹c; a=b=90^o, g=120^o

Решетка
примитивная	базо-центрированная	объемно-центрированная	гране-центрированная
Триклинная сингония

Моноклинная сингония

Ромбическая сингония

Тетрагональная сингония

Тригональная (ромбоэдрическая) сингония

Гексагональная сингония

Кубическая сингония

Рис.1.6. Пространственные решетки Браве


а	б
Рис.1.7. Примитивные ячейки для ОЦК (а) и ГЦК (б) решеток

Параметры	Тип решетки
Прими- тивная	ОЦК	ГЦК	Типа алмаза
Координационное число
Атомный радиус
Число атомов в элементарной ячейке
Коэффициент упаковки η (плотность упаковки), %