Точечные группы симметрии

Как уже было отмечено, точечная группа (класс) симметрии кристалла является совокупностью операций симметрии, которая совмещает кристалл с самим собой, при которых одна (особенная) точка кристалла остается неподвижной (трансляции отсутствуют). Точечные группы описывают внешнюю форму (огранку) кристалла. Симметрия внешней формы кристалла определяется симметрией его атомного строения, которое обусловливает и симметрию физических свойств кристалла (диэлектрических, магнитных и др.).

Для каждой точечной группы можно выделить минимум исходных элементов, необходимых для выведения всей совокупности элементов. Порядок группы определяется количеством элементов, которые в нее входят.

Операциями точечной симметрии является: повороты вокруг оси симметрии порядка 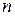на угол , отражение в плоскости симметрии (зеркальное отражение), инверсия (симметрия относительно точки), инверсные повороты . Вместо инверсионных поворотов иногда рассматривают зеркальные повороты . Геометрически возможные сочетания этих операций определяют ту или другую точечную группу симметрии.

Рассмотрим действие инверсионных осей симметрии. Инверсионная ось симметрии представляет собой совместное действие – произведение оси симметрии и центра симметрии: . При этом должны возникать качественно новые элементы симметрии. Но не все такие образованные элементы симметрии являются новыми. Например, инверсионная ось симметрии первого порядка эквивалентна центру симметрии (центру инверсии); действие инверсионной оси второго порядка тождественно плоскости симметрии, которая перпендикулярна оси; операция эквивалентна действию оси третьего порядка и центра симметрии; операция 6 также не дает новый элемент симметрии, поскольку эквивалентна последовательному действию оси третьего порядка и плоскости симметрии. Такое свойство имеет только ось 4 (рис.1.3). В данном случае грань А возвращается на 90⁰ в промежуточное состояние и отражается в центре, переходя в грань В. Отметим также, что инверсионная ось четного порядка 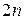одновременно является простой осью симметрии порядка .

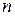Рис.1.3. Действие инверсионной оси четвертого порядка

Следовательно, внешняя симметрия кристаллических многогранников полностью описывается операциями симметрии: .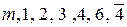

Кристаллы по симметрии разделяют на категории, используя понятие единичного направления, то есть такого, которое не повторяется в кристаллическом многограннике. Его еще называют особенным. Всего существует три категории, каждая из которых включает несколько сингоний. В определенную сингонию попадают кристаллы с одинаковой симметрией элементарных ячеек и одинаковой системой координат. Всего существуют 7 сингоний.

К высшей категории относится лишь одна сингония – кубическая. Оси параллельны трем взаимно перпендикулярным осям симметрии 4, или , или 2 порядка.

К средней категории относятся три сингонии:

– тригональная; за ось принимают ось симметрии 3 или порядка, оси и 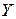лежат в плоскости, которая перпендикулярна к , и совпадают с осями 2 порядка или перпендикулярны к плоскостям симметрии (если такие есть);

– тетрагональная; за ось принимают ось симметрии 4 или порядка, оси и 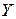лежат в плоскости, которая перпендикулярна к , и совпадают с осями 2 порядка или перпендикулярны к плоскостям симметрии (если такие есть);

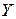– гексагональная; тетрагональная; за ось принимают ось симметрии 6 или порядка, ось и лежат в плоскости, которая перпендикулярна к , и совпадают с осями 2 порядка или перпендикулярные к плоскостям симметрии (если такие есть).

К низшей категории также принадлежат три сингонии:

– ромбическая; ось выбирают параллельно осям симметрии 2 или вдоль перпендикуляров к плоскостям симметрии;

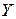– моноклинная; ось выбирают вдоль оси симметрии 2, или вдоль перпендикуляра к плоскости симметрии, оси и лежат в плоскости, которая перпендикулярна к оси 2;

– триклинная; оси кристаллографической системы не заданы элементами симметрии, а выбраны вдоль ребер кристалла или элементарной ячейки при условии .

Для идеальных кристаллических многогранников существует 32 точечных группы симметрии, которые разделяются на два класса. К первому классу принадлежит 27 групп, в которых присутствует ось 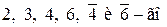порядка.

Ко второму классу относят группы, в которых есть несколько осей порядка . Их называют группами кубической симметрии, существуют 5 таких групп.

Функции, которые описывают зависимость различных свойств кристалла от направления, имеют определенную точечную симметрию, которая однозначно связана с группой симметрии огранки кристалла.

Многие свойства кристаллов, которые принадлежат к определенным точечным группам симметрии, описываются так называемыми предельными группами симметрии – группами Кюри[3]. Они обладают осью симметрии бесконечного порядка, которая отражается символом . Наличие оси означает, что объект совмещается с собой при повороте на любой угол, в том числе на бесконечно малый угол. Известно семь групп Кюри, для наглядности их изображают с помощью фигур конечных размеров, которые представляют собой тела вращения (рис.1.4).

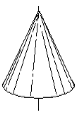
Группа содержит только одну ось бесконечного порядка. Ей отвечает конус, который равномерно вращающийся влево или вправо. Ось симметрии полярная (полярным называется направление, концы которого физически и геометрически неэквивалентные).

Группа 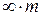имеет ось бесконечного порядка и бесконечное число продольных плоскостей симметрии и ей отвечает неподвижный конус. Ось симметрии полярная. Такой симметрией обладают полярные векторы, например, электрическое поле, сила, ускорение и др.

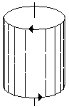
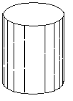
Группа имеет ось бесконечного порядка, поперечную плоскость симметрии и центр. Это симметрия вращающегося цилиндра. Этой симметрией обладает постоянное магнитное поле или поле проводника с током.

Группа 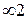содержит ось бесконечного порядка бесконечное число осей 2, перпендикулярных к оси . Ей отвечает цилиндр с вращающимися в разных направлениях концами. Такая симметрия характерна для явления удельного вращения плоскостей поляризации.

Группа 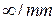, которой отвечает неподвижный цилиндр, содержит ось бесконечного порядка, бесконечное количество продольных плоскостей симметрии, осей 2-го порядка и центр инверсии. Такой симметрией обладает одноосное давление.

Группа содержит бесконечное число осей симметрии без плоскостей и центра симметрии. Ей отвечает шар, у которого все диаметры закручены по правому (или левому) винту. Такая симметрия удельного вращения плоскостей поляризации в изотропной среде.

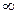
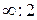
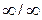
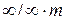
Рис.1.4. Фигуры, которые имеют форму предельных групп симметрии

Группа 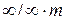– симметрия шара. Содержит центр симметрии, бесконечное число осей симметрии порядка и бесконечное число плоскостей симметрии. Это симметрия полей гидростатического давления, однородного нагрева.

32 кристаллографических и 7 предельных классов – это 39 возможных типов проявления анизотропии в физических свойствах кристаллов. Класс характеризуется предельной анизотропией. В классах и 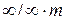все направления эквивалентны и анизотропия в них невозможна. В каждом из 36 оставшихся классов на анизотропию тех или других физических свойств накладываются определенные ограничения.